G4: Verschobene Normalparabeln der Form f(x)=x²+e: Unterschied zwischen den Versionen
Aus KAS-Wiki
| Zeile 18: | Zeile 18: | ||
Scheitelpunkt: S(0/e) | Scheitelpunkt: S(0/e) | ||
| + | |||
| + | |||
| + | Die verschobene Normalparabel kann sowohl in den positven wie auch in den negativen verschoben werden. | ||
| + | Wenn '''e negativ (-e)''' ist so ist sie in den '''negativen bereich''' verschoben. Wenn '''e positv (e)''' ist so ist sie nach oben verschoben. | ||
Version vom 16. Dezember 2009, 09:23 Uhr
Verschobene Normalparabel der Form f(x)=x²+e
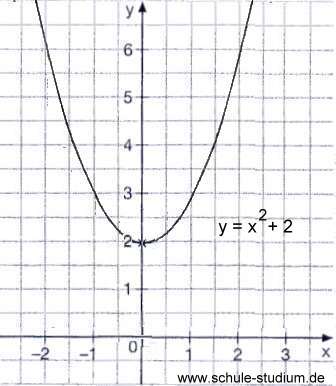
Die verschobene Normalparabel der Form "f(x)=x²+e" ist parallel der Y-Achse verschoben. Sie ist nach oben verschoben wenn e>0 ist und nach unten verschoben wenn e<0 ist.
links: Die normalparbel ist um 2 nach oben auf der Y-Achse verschoben
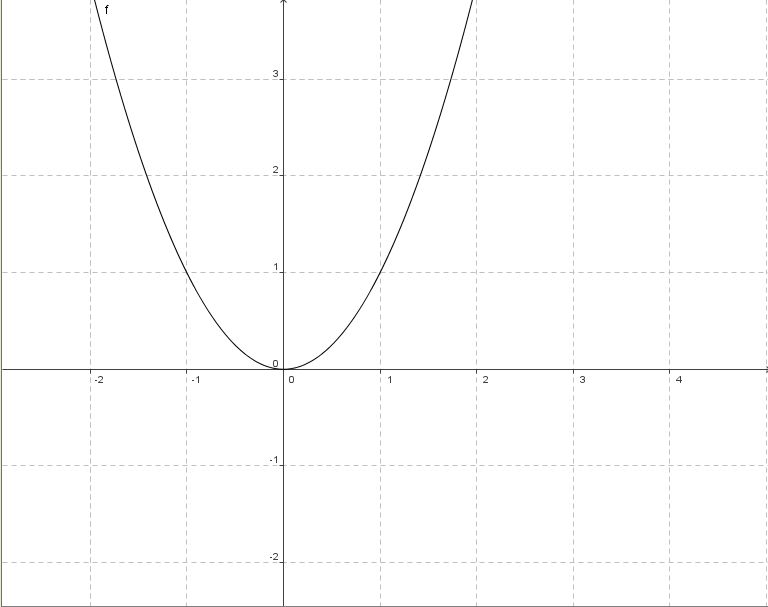
rechts: Das ist eine Normalparabel
Die verschobene Normalparabel:
Symmetrieachse: y-Achse
Scheitelpunkt: S(0/e)
Die verschobene Normalparabel kann sowohl in den positven wie auch in den negativen verschoben werden.
Wenn e negativ (-e) ist so ist sie in den negativen bereich verschoben. Wenn e positv (e) ist so ist sie nach oben verschoben.