Linsengesetz (Maike H, Alina): Unterschied zwischen den Versionen
(→Formel) |
(→Ergebnis) |
||
| (61 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
== Einleitung == | == Einleitung == | ||
| − | Die Größe und die Lage eines Bildes hängt von der Entfernung ab. Das erkennt man z.B. wenn man fotografiert. Je weiter man von dem Objekt entfernt steht, desto kleiner erscheint es auf der Kamera. Mit | + | Die Größe und die Lage eines Bildes hängt von der Entfernung ab. Das erkennt man z.B. wenn man fotografiert. Je weiter man von dem Objekt entfernt steht, desto kleiner erscheint es auf der Kamera. Mit der Linsengleichung kann man diese Abstände berechnen. Die Größe des Bildes wird zwar nicht von der Linsengleichung erfasst, kann aber mit dem [[Abbildungsgesetz (Tobias, Dario)|Abbildungsgesetz]] berechnet werden. |
==Formel== | ==Formel== | ||
| − | Die Formel | + | Die Formel der Linsengleichung lautet:.<br /> |
| − | <math>\frac{1} {b} +\frac{1} {g} =\frac{1} {f} </math> | + | <math>\frac{1} {b} +\frac{1} {g} =\frac{1} {f} </math>.<br /> |
| − | f = Brennweite | + | f = Brennweite<br /> |
| − | g = Gegenstandsweite | + | g = Gegenstandsweite<br /> |
| − | b = Bildweite | + | b = Bildweite<br /> |
| − | G = Gegenstand | + | G = Gegenstand<br /> |
B = Bildgröße | B = Bildgröße | ||
| + | |||
| + | ==Experiment== | ||
| + | |||
| + | In dem folgenden Experiment stellen wir eine Möglichkeit vor, wie man die Linsengleichung anwenden kann.<br /> | ||
| + | Hierbei überprüfen wir unser Ergebnis am Ende mithilfe der Linsengleichung | ||
| + | |||
| + | ==Material== | ||
| + | |||
| + | *Kerze<br /> | ||
| + | *Linse<br /> | ||
| + | *Mattscheibe<br /> | ||
| + | *Lineal | ||
| + | |||
| + | ==Durchführung== | ||
| + | |||
| + | Bei dem Experiment ist f = 5cm.<br /> | ||
| + | Um g und b herauszufinden bauen wir zuerst ein System aus der Kerze, der Linse und der Mattscheibe auf.<br /> | ||
| + | [[image:Ph aple.JPG|250px]].<br /> | ||
| + | Dann verändern wir die Abstände zwischen Kerze und Linse und Linse und Mattscheibe (siehe Bild)<br /> bis auf der Mattscheibe ein scharfes Bild der Kerze entsteht.<br /> | ||
| + | Jetzt messen wir die Abstände für g und b. | ||
| + | |||
| + | ==Ergebnis== | ||
| + | |||
| + | [[Datei:Sammellinse Skizze.png|framed|300px|reelles Bild bei einer [http://de.wikipedia.org/wiki/Sammellinse konvexen Linse]]] | ||
| + | |||
| + | Für b messen wir einen Abstand von ungefähr 8 cm.<br /> | ||
| + | Für g beträgt der Abstand ungefähr 10 cm.<br /> | ||
| + | Dies überprüfen wir indem wir die Werte einsetzen und dann ausrechnen: 1:8 + 1:10.<br /> | ||
| + | Für 1/f ergibt sich ein Wert von 0.2.<br /> | ||
| + | Das überprüfen wir indem wir 1:5 (Brennweite) rechnen.<br /> | ||
| + | Das Ergebnis ist ebenfalls 0.2.<br /> | ||
| + | Somit haben wir die Linsengleichung bestätigt. | ||
| + | |||
| + | ==Anwendung== | ||
| + | |||
| + | Linsen werden sowohl für Teleskope als auch für Mikroskope angewendet.<br /> | ||
| + | Es gibt zum Besipiel ein sogenanntes Linsenteleskop. Es ist das älteste Teleskop der Welt. | ||
| + | |||
| + | ==Quellen== | ||
| + | |||
| + | * Fokus Physik Gymnasium 7|8, Cornelsen Verlag, Berlin 2010<br /> | ||
| + | * [http://de.wikipedia.org/wiki/Linsengleichung Linsengleichung] | ||
Aktuelle Version vom 12. Dezember 2011, 10:48 Uhr
Inhaltsverzeichnis |
Einleitung
Die Größe und die Lage eines Bildes hängt von der Entfernung ab. Das erkennt man z.B. wenn man fotografiert. Je weiter man von dem Objekt entfernt steht, desto kleiner erscheint es auf der Kamera. Mit der Linsengleichung kann man diese Abstände berechnen. Die Größe des Bildes wird zwar nicht von der Linsengleichung erfasst, kann aber mit dem Abbildungsgesetz berechnet werden.
Formel
Die Formel der Linsengleichung lautet:.
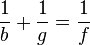 .
.
f = Brennweite
g = Gegenstandsweite
b = Bildweite
G = Gegenstand
B = Bildgröße
Experiment
In dem folgenden Experiment stellen wir eine Möglichkeit vor, wie man die Linsengleichung anwenden kann.
Hierbei überprüfen wir unser Ergebnis am Ende mithilfe der Linsengleichung
Material
- Kerze
- Linse
- Mattscheibe
- Lineal
Durchführung
Bei dem Experiment ist f = 5cm.
Um g und b herauszufinden bauen wir zuerst ein System aus der Kerze, der Linse und der Mattscheibe auf.

Dann verändern wir die Abstände zwischen Kerze und Linse und Linse und Mattscheibe (siehe Bild)
bis auf der Mattscheibe ein scharfes Bild der Kerze entsteht.
Jetzt messen wir die Abstände für g und b.
Ergebnis
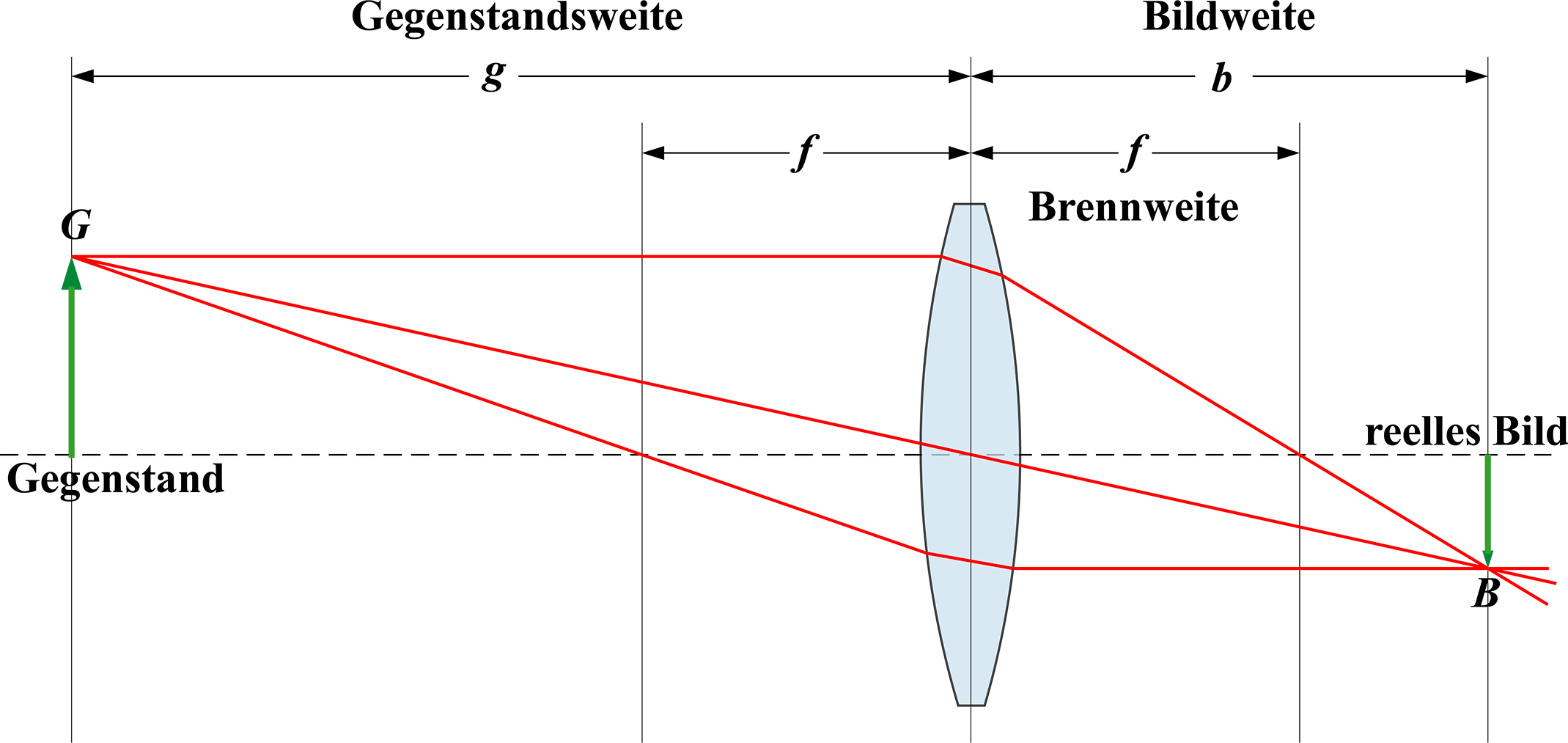
Für b messen wir einen Abstand von ungefähr 8 cm.
Für g beträgt der Abstand ungefähr 10 cm.
Dies überprüfen wir indem wir die Werte einsetzen und dann ausrechnen: 1:8 + 1:10.
Für 1/f ergibt sich ein Wert von 0.2.
Das überprüfen wir indem wir 1:5 (Brennweite) rechnen.
Das Ergebnis ist ebenfalls 0.2.
Somit haben wir die Linsengleichung bestätigt.
Anwendung
Linsen werden sowohl für Teleskope als auch für Mikroskope angewendet.
Es gibt zum Besipiel ein sogenanntes Linsenteleskop. Es ist das älteste Teleskop der Welt.
Quellen
- Fokus Physik Gymnasium 7|8, Cornelsen Verlag, Berlin 2010
- Linsengleichung

