Lösung linearer Gleichungssysteme.: Unterschied zwischen den Versionen
Chris1 (Diskussion | Beiträge) (→Besonderes) |
Chris1 (Diskussion | Beiträge) (→Gaußches Eliminierungsverfahren) |
||
| Zeile 6: | Zeile 6: | ||
* Addition/Subtraktion des Vielfachen einer Gleichung mit einer anderen Gleichung | * Addition/Subtraktion des Vielfachen einer Gleichung mit einer anderen Gleichung | ||
| + | === Bedingung === | ||
| + | Man braucht mindestens genauso viele Gleichungen, wie unbekannte Variablen. | ||
| + | Wenn es mehr Gleichungen sind, muss man mit der/den "überflüssigen" Gleichung(en) die Variablen einsetzen und das Ergebniss überprüfen. Wenn die Zahlen nicht übereinsstimmen, gibt es kein Ergebniss. | ||
=== Beispiel === | === Beispiel === | ||
Version vom 18. Dezember 2009, 11:37 Uhr
Inhaltsverzeichnis[Verbergen] |
Gaußches Eliminierungsverfahren
Die Operationen
- Multiplikation einer Gleichung mit einem Faktor
- Addition/Subtraktion des Vielfachen einer Gleichung mit einer anderen Gleichung
Bedingung
Man braucht mindestens genauso viele Gleichungen, wie unbekannte Variablen. Wenn es mehr Gleichungen sind, muss man mit der/den "überflüssigen" Gleichung(en) die Variablen einsetzen und das Ergebniss überprüfen. Wenn die Zahlen nicht übereinsstimmen, gibt es kein Ergebniss.
Beispiel
Aufstellen des linearen Gleichungssystems.
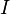
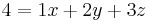
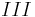
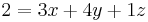
Durch das Subtraktionsverfahren eliminiert man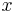 
aus 2 Gleichungen
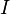
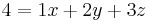
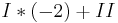
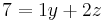
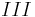
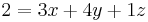
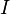
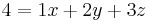
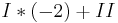
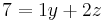
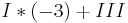
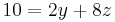
Durch erneute Subtraktion wird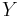 
eliminiert.
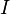
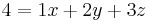
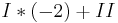
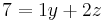
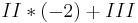
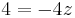
Durch Einsetzten und Lösen erhält man:
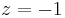
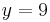
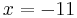
Besonderes
1.Beispiel
Hätte man als Gleichungen:
1. Gleichung: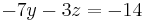 
2. Gleichung: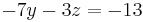 
hätte man nach dem Gleichsetzen das Ergebniss: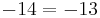 
In solchen Fällen gibt es keine Lösung.
2.Beispiel
Hätte man jedoch die GLeichungen:
1. Gleichung: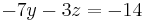
2. Gleichung: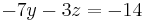
hätte man das Ergebniss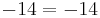 
In solchen Fällen gibt es unendlich viele Lösungen.
