Ganzrationale Funktionen.: Unterschied zwischen den Versionen

Version vom 18. Dezember 2009, 10:55 Uhr

Ganzrationale Funktionen

f(x) = a_nxⁿ + a_n-1x^n-1 + ... + a₁x + a₀

n = Grad des Polynoms

Definitionsbereich:

• 
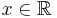
• (a_n 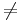0, )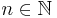

Bestimmung einer ganzrationalen Funktion in Sachzusammenhängen:

• lineares Gleichungssystem aufstellen und lösen
• Koordinatensystem auswählen
• Bedingung: n + 1 Bedingungen sind nötig

Nullstellen der Funktion:

f(x)=0

Funktionen 2. Grades:

Gleichung f(x)=0 in die Normalform umwandeln:

f(x)= ax² + bx + c | :a

   = x2 +  x + 

• Lösen der Gleichung mithilfe der p/q-Formel:

f(x) = 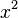+ px + q = 0

=

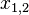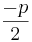
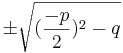
oder c ist gleich 0:
ax²+bx= 0 | x ausklammern
x(ax+b) = 0
dann:
ax+b = 0

Funktionen 3. Grades:

f(x)= a³x + b²x + cx+d

• Lösen der Gleichung mithilfe der Polynomdivision:

• Hilfe: Wenn es eine ganzzeilige Nullstelle gibt, dann muss diese Nullstelle Teiler des ganzen Glieds sein.

Funktionen mehrstelligem Grades:

• Z.B. f(x) = ax⁸ + bx⁴ + cx²

• Lösen der Gleichung mithilfe der Substitution:

• x² ausklammern: f(x) = x² * (ax⁴ + bx² + c)

• für x² = z

• daraus ergibt sich: f(z) = az⁴ + bz² + cz

• Gleichung lösen und danach wieder zurück substituieren

Symmetrie:

• Wenn alle Exponenten gerade sind, dann ist die Funktion achsensymmetrisch zur y- Achse
• Wenn mind. ein Exponent ungerade ist, dann ist die Funkton punktsymmetrisch zum Ursprung

Verhalten von ganzrationalen Funktionen: