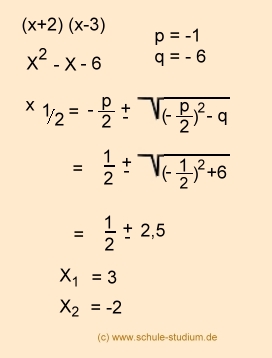G14: Lösen quadratischer Gleichungen: Unterschied zwischen den Versionen
(→Lösen mit der p-q-Formel) |
(→Lösen mit der p-q-Formel) |
||
| Zeile 16: | Zeile 16: | ||
===Lösen mit der p-q-Formel=== | ===Lösen mit der p-q-Formel=== | ||
| − | Wenn man die qudratische Gleichung mit der p-q-Formel lösen möchte, sollte man den folgnden Weg benutzen: | + | Wenn man die qudratische Gleichung mit der p-q-Formel lösen möchte, sollte man den folgnden Weg benutzen um die unbekannten Variablen zu errechnen: |
[[Bild:pq-Formel.jpg]] | [[Bild:pq-Formel.jpg]] | ||
| + | |||
Ein Video zur besseren Erläuterung[http://www.youtube.com/watch?v=4grbGixuSXM] | Ein Video zur besseren Erläuterung[http://www.youtube.com/watch?v=4grbGixuSXM] | ||
| + | |||
| + | |||
| + | Anschließend sollte man noch die Probe machen, um sicher zu gehen, dass man keinen Rechenfehler gemacht hat. | ||
Version vom 22. Dezember 2009, 10:24 Uhr
Definition quadratischer Gleichungen
Wenn in einer ganzrationalen Gleichung, ohne x im Nenner von Brüchen, die Unbekannte mit der Hochzahl 2 auftritt, also z.B. als x², und dieses x² auch nicht durch Umformungen wegfällt, spricht man von einer quadratischen Gleichung. Bei dieser kommt die Variable x mindestens einmal in der 2.Potenz vor, aber nicht höher. Die Normalform der qudratischen Gleichung ist immer: ax² + px + q = 0
Natürlich darf die Variable a nicht gleich Null sein, denn dann würde der erste Summand wegfallen, und es würde eine lineare Gleichung vorliegen:
0·x2+8x+9=0 = 8x+9=0
Lösungsvarianten
Es giebt zwei verschiedene Varianten die quadratische Gleichung zu Lösen.
Lösen mit der p-q-Formel
Wenn man die qudratische Gleichung mit der p-q-Formel lösen möchte, sollte man den folgnden Weg benutzen um die unbekannten Variablen zu errechnen:
Ein Video zur besseren Erläuterung[1]
Anschließend sollte man noch die Probe machen, um sicher zu gehen, dass man keinen Rechenfehler gemacht hat.