Linsengesetz (Lara, Lioba): Unterschied zwischen den Versionen
(→Durchführung) |
|||
| (30 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
==Einleitung== | ==Einleitung== | ||
| − | Mit dem Linsengesetz kann man die optische Abbildung einer idealen Linse berechnen. | + | Mit dem Linsengesetz kann man die optische Abbildung einer idealen Linse berechnen. Die Funktion eines Fotoapparates beruht auf dem Linsengesetz.Die Größe des Bildes wird zwar nicht von der Linsengleichung erfasst, kann aber mit dem Abbildungsgesetz berechnet werden. |
| + | |||
| + | ==Anwendung== | ||
| + | |||
| + | Beim Mikroskop benutzt man die Linsengleichung um den richtigen Abstand zu erfassen. | ||
==Formel== | ==Formel== | ||
| + | |||
| + | [[Image:Sammellinse Skizze.png|600px|thumb|right]] | ||
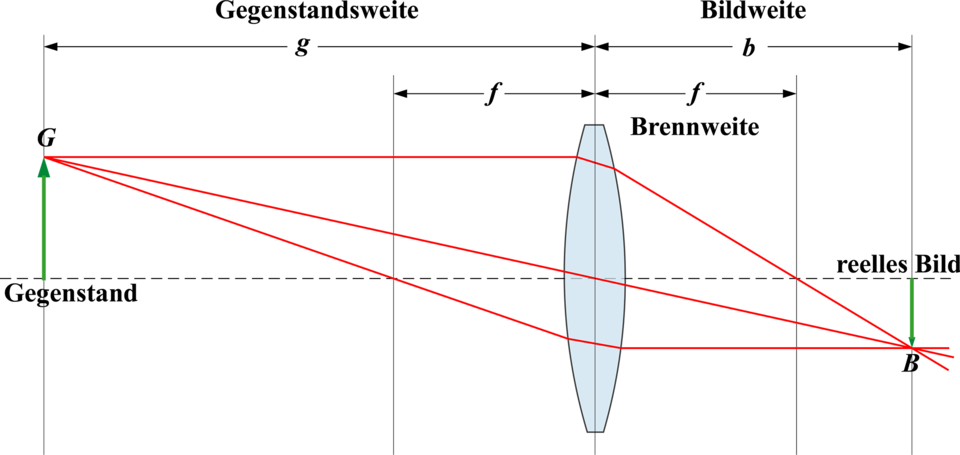
Die Formel für das Linsengesetz lautet wie folgt: | Die Formel für das Linsengesetz lautet wie folgt: | ||
<math>\frac{1} {b} +\frac{1} {g} =\frac{1} {f} </math> | <math>\frac{1} {b} +\frac{1} {g} =\frac{1} {f} </math> | ||
| − | |||
| − | |||
* g: Gegenstandsweite zwischen Kerze und Linse.<br /> | * g: Gegenstandsweite zwischen Kerze und Linse.<br /> | ||
| Zeile 15: | Zeile 19: | ||
* B: Bildgröße.<br /> | * B: Bildgröße.<br /> | ||
* f: Brennweite der Linse. | * f: Brennweite der Linse. | ||
| + | |||
| + | ==Berechnung== | ||
| + | Wenn man g oder b berechnen will kann man die umgestellte Gleichung benutzen | ||
==Materialien== | ==Materialien== | ||
| Zeile 24: | Zeile 31: | ||
* eine Mattscheibe.<br /> | * eine Mattscheibe.<br /> | ||
| − | * Zusätzlich | + | * Zusätzlich kann man ein Lineal verwenden um den richtigen Abstand abzumessen. |
==Durchführung== | ==Durchführung== | ||
| Zeile 30: | Zeile 37: | ||
[[Datei:Physik_022.JPG|300px|thumb|right|Versuchsaufbau]] | [[Datei:Physik_022.JPG|300px|thumb|right|Versuchsaufbau]] | ||
| − | + | Eine Linse wird zwischen eine Kerze und eine Mattscheibe gestellt. Der Abstand zwischen Kerze, Linse und Mattscheibe wird verändert, bis ein scharfes Bild der Kerzenflamme auf der Mattscheibe entsteht.Dabei muss die Brennweite der Linse 5cm betragen. | |
==Ergebnis== | ==Ergebnis== | ||
| − | Bei Abschluss des Experimentes betrug die Gegenstandsweite g 8cm und die Bildweite b 12cm. | + | Bei Abschluss des dargestellten Experimentes betrug die Gegenstandsweite g 8cm und die Bildweite b 12cm, daraus ergibt sich für |
| − | So | + | 1/f 0,2cm. <br /> |
| + | So war das umgedrehte Bild der Kerzenflamme auf der Mattscheibe deutlich zu erkennen. | ||
| + | Beim Einsetzen nach g und b und Auflösen von f hat sich die Linsengleichung bestätigt. | ||
| + | |||
| + | ==Quellen und Weblinks== | ||
| + | |||
| + | *Fokus Physik Gymnasium 7/8 (erschienen im Cornelsen Verlag)<br /> | ||
| + | *http://de.wikipedia.org/wiki/Linsengleichung<br /> | ||
| + | *[http://de.wikipedia.org/wiki/Kategorie:Paraxiale_Optik Paraxiale Optik] | ||
Aktuelle Version vom 10. September 2012, 10:56 Uhr
Inhaltsverzeichnis[Verbergen] |
Einleitung
Mit dem Linsengesetz kann man die optische Abbildung einer idealen Linse berechnen. Die Funktion eines Fotoapparates beruht auf dem Linsengesetz.Die Größe des Bildes wird zwar nicht von der Linsengleichung erfasst, kann aber mit dem Abbildungsgesetz berechnet werden.
Anwendung
Beim Mikroskop benutzt man die Linsengleichung um den richtigen Abstand zu erfassen.
Formel
Die Formel für das Linsengesetz lautet wie folgt:
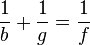
- g: Gegenstandsweite zwischen Kerze und Linse.
- b: Bildweite zwischen Linse und Mattscheibe.
- G: Der Gegenstand ( Kerze).
- B: Bildgröße.
- f: Brennweite der Linse.
Berechnung
Wenn man g oder b berechnen will kann man die umgestellte Gleichung benutzen
Materialien
Die Materialien für das folgende Experiment sind:.
- eine Kerze.
- eine Linse.
- eine Mattscheibe.
- Zusätzlich kann man ein Lineal verwenden um den richtigen Abstand abzumessen.
Durchführung
Eine Linse wird zwischen eine Kerze und eine Mattscheibe gestellt. Der Abstand zwischen Kerze, Linse und Mattscheibe wird verändert, bis ein scharfes Bild der Kerzenflamme auf der Mattscheibe entsteht.Dabei muss die Brennweite der Linse 5cm betragen.
Ergebnis
Bei Abschluss des dargestellten Experimentes betrug die Gegenstandsweite g 8cm und die Bildweite b 12cm, daraus ergibt sich für
1/f 0,2cm.
So war das umgedrehte Bild der Kerzenflamme auf der Mattscheibe deutlich zu erkennen.
Beim Einsetzen nach g und b und Auflösen von f hat sich die Linsengleichung bestätigt.
Quellen und Weblinks
- Fokus Physik Gymnasium 7/8 (erschienen im Cornelsen Verlag)
- http://de.wikipedia.org/wiki/Linsengleichung
- Paraxiale Optik