GK Bugaj 2015: Unterschied zwischen den Versionen
Aus KAS-Wiki
Rbugaj (Diskussion | Beiträge) (→Zur Übung) |
Rbugaj (Diskussion | Beiträge) (→Zur Übung) |
||
| Zeile 17: | Zeile 17: | ||
=Zur Übung= | =Zur Übung= | ||
| − | Bestimme die | + | Bestimme die Extremstellen der Funktionen |
<math>f(x)=0,5x^2-2x</math>, | <math>f(x)=0,5x^2-2x</math>, | ||
| Zeile 26: | Zeile 26: | ||
<math>h(x)=x^5+x^3</math>. | <math>h(x)=x^5+x^3</math>. | ||
| + | |||
| + | Gib außerdem an, ob es sich an dieser Stelle um Hoch- oder Tiefpunkte handelt. | ||
Version vom 10. Februar 2015, 19:22 Uhr
Mit den folgenden GeoGebra-Arbeitsblättern soll erarbeitet werden, wie die Extrempunkte (Hoch- und Tiefpunkte) einer Funktion ermittelt werden können.
Inhaltsverzeichnis |
Arbeitsauftrag 1
Öffne dazu diesen Link und das dort hinterlegte Arbeitsblatt.
- Verschiebe den Punkt entlang des Funktionsgraphen und beobachte, wie sich die Tangentensteigung verändert.
- Fertige eine Tabelle an, aus der der Wert(ebereich) der Steigung abschnittsweise abgelesen werden kann (zur Hilfe kannst du den Schalter "Intervallgrenzen anzeigen" aktivieren).
- Überlege dir, in welchem Zusammenhang die Tangentensteigung mit der Funktion steht.
Arbeitsauftrag 2
Öffne nun diesen Link und das dort hinterlegte Arbeitsblatt.
- Verschiebe den Punkt entlang des Funktionsgraphen und beobachte, wie sich die Tangentensteigung verändert.
- Fertige eine Tabelle an, aus der der Wert(ebereich) der Steigung abschnittsweise abgelesen werden kann (zur Hilfe kannst du den Schalter "Intervallgrenzen anzeigen" aktivieren).
- Worin besteht der Unterschied zum Beispiel aus Aufgabe 1?
Arbeitsauftrag 3
Überlege dir, wie du mit deinen Ergebnissen aus Aufgabe 1 und 2 ein (formales) Kriterium für die Bestimmung von Extrempunkten formulieren kannst.
Zur Übung
Bestimme die Extremstellen der Funktionen
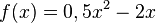 ,
,
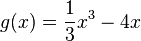
und
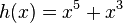 .
.
Gib außerdem an, ob es sich an dieser Stelle um Hoch- oder Tiefpunkte handelt.

