Gemeinsame Punkte einer Funktionsschar.: Unterschied zwischen den Versionen

Aus KAS-Wiki
Wechseln zu: Navigation, Suche
Zeile 6: Zeile 6:
 
Beispielfuntionsschar:
 
Beispielfuntionsschar:
 
<br />f(x)=2kx³+(2-4k)x
 
<br />f(x)=2kx³+(2-4k)x
−
<br />=>Wir setzen f(x) für k<sub>1</sub> und k<sub>2</sub> gleich.
+
<br />
−
<br />2k<sub>1</sub>x³+(2-4k<sub>1</sub>)x=2k<sub>2</sub>x³+(2-4k<sub>2</sub>)x
+

Version vom 23. November 2010, 13:50 Uhr

Gemeinsame Punkte einer Schar bedeutet das fk(x) Punkte hat, die von k unabhängig sind. Man sucht gemeinsame Punkte von zwei Funktionen fk(x) bei denen k1 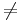\not= k2.
Das bedeutet:
fk1(x)=fk2(x)

Beispielfuntionsschar:
f(x)=2kx³+(2-4k)x

Von „http://kas.zum.de/index.php?title=Gemeinsame_Punkte_einer_Funktionsschar.&oldid=4844“