Gemeinsame Punkte einer Funktionsschar.: Unterschied zwischen den Versionen
Aus KAS-Wiki
Moritz (Diskussion | Beiträge) |
Moritz (Diskussion | Beiträge) |
||
| Zeile 1: | Zeile 1: | ||
Gemeinsame Punkte einer Schar bedeutet das '''f<sub>k</sub>(x)''' Punkte hat, die von '''k''' unabhängig sind. | Gemeinsame Punkte einer Schar bedeutet das '''f<sub>k</sub>(x)''' Punkte hat, die von '''k''' unabhängig sind. | ||
Man sucht gemeinsame Punkte von zwei Funktionen f<sub>k</sub>(x) bei denen '''k<sub>1</sub> <math>\not=</math> k<sub>2</sub>.''' | Man sucht gemeinsame Punkte von zwei Funktionen f<sub>k</sub>(x) bei denen '''k<sub>1</sub> <math>\not=</math> k<sub>2</sub>.''' | ||
| − | <br />Das bedeutet: | + | '''<br />Das bedeutet:''' |
<br />f<sub>k1</sub>(x)=f<sub>k2</sub>(x) | <br />f<sub>k1</sub>(x)=f<sub>k2</sub>(x) | ||
| − | Beispielfuntionsschar: | + | '''Beispielfuntionsschar:''' |
<br />f<sub>k</sub>(x)=2kx<sup>2</sup>+4xk+5 | <br />f<sub>k</sub>(x)=2kx<sup>2</sup>+4xk+5 | ||
| Zeile 13: | Zeile 13: | ||
<br /><=>x(2k<sub>1</sub>x-2k<sub>2</sub>x+4k<sub>1</sub>-4k<sub>2</sub>)=0 | <br /><=>x(2k<sub>1</sub>x-2k<sub>2</sub>x+4k<sub>1</sub>-4k<sub>2</sub>)=0 | ||
<br /><=>x<sub>1</sub>=0 v. 0=2k<sub>1</sub>x-2k<sub>2</sub>x+4k<sub>1</sub>-4k<sub>2</sub> | <br /><=>x<sub>1</sub>=0 v. 0=2k<sub>1</sub>x-2k<sub>2</sub>x+4k<sub>1</sub>-4k<sub>2</sub> | ||
| + | <br /> | ||
Für den Term 0=2k<sub>1</sub>x-2k<sub>2</sub>x+4k<sub>1</sub>-4k<sub>2</sub> gibt es keine Lösung die unabhängig von k ist. | Für den Term 0=2k<sub>1</sub>x-2k<sub>2</sub>x+4k<sub>1</sub>-4k<sub>2</sub> gibt es keine Lösung die unabhängig von k ist. | ||
| − | Durch die Bedingung k<sub>1</sub> <math>\not=</math> k<sub>2</sub> bleibt x<sub>1</sub>=0 die einzige Lösung. | + | Durch die Bedingung k<sub>1</sub> <math>\not=</math> k<sub>2</sub> bleibt '''x<sub>1</sub>=0''' die einzige Lösung. |
| − | + | <br /> | |
| − | f(0)=5 | + | <br />=>f(0)=5 |
Der gemeinsame Punkt der Schar f<sub>k</sub>(x) liegt bei P(0/5) | Der gemeinsame Punkt der Schar f<sub>k</sub>(x) liegt bei P(0/5) | ||
Version vom 28. November 2010, 18:26 Uhr
Gemeinsame Punkte einer Schar bedeutet das fk(x) Punkte hat, die von k unabhängig sind.
Man sucht gemeinsame Punkte von zwei Funktionen fk(x) bei denen k1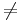 
k2.
Das bedeutet:
fk1(x)=fk2(x)
Beispielfuntionsschar:
fk(x)=2kx2+4xk+5
Wir setzen fk1(x) mit fk2(x)gleich und lösen sie auf:
2k1x2++4xk1+5=2k2x2+4xk2+5
<=>2k1x2+4xk1-2k2x2-4xk2=0
<=>x(2k1x-2k2x+4k1-4k2)=0
<=>x1=0 v. 0=2k1x-2k2x+4k1-4k2
Für den Term 0=2k1x-2k2x+4k1-4k2 gibt es keine Lösung die unabhängig von k ist.
Durch die Bedingung k1 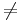k2 bleibt x1=0 die einzige Lösung.
=>f(0)=5
Der gemeinsame Punkt der Schar fk(x) liegt bei P(0/5)
