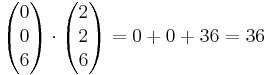Spatprodukt.: Unterschied zwischen den Versionen
Aus KAS-Wiki
(Die Seite wurde neu angelegt: Mit dem Spatprodukt berechnet man das Volumen eines durch drei Vektoren aufgespannten Spats. Die allgemeine Formel lautet: <math>V_{\vec{a},\vec{b},\vec{c}} = (\vec{a}...) |
|||
| Zeile 8: | Zeile 8: | ||
Berechne das Volumen des Spat, das durch die Vektoren <math>\vec a</math>=<math>\begin{pmatrix} | Berechne das Volumen des Spat, das durch die Vektoren <math>\vec a</math>=<math>\begin{pmatrix} | ||
2 \\4 \\0 \end{pmatrix}</math> , <math>\vec b</math>= <math>\begin{pmatrix} | 2 \\4 \\0 \end{pmatrix}</math> , <math>\vec b</math>= <math>\begin{pmatrix} | ||
| − | 0 \\3 \\0 \end{pmatrix}</math> und <math>\vec c</math>= <math>\begin{pmatrix}2 \\2 \\6 \end{pmatrix}</math> | + | 0 \\3 \\0 \end{pmatrix}</math> und <math>\vec c</math>= <math>\begin{pmatrix}2 \\2 \\6 \end{pmatrix}</math> aufgespannt wird. |
Also <math>V_{\vec{a},\vec{b},\vec{c}} = | Also <math>V_{\vec{a},\vec{b},\vec{c}} = | ||
Version vom 17. Dezember 2010, 11:24 Uhr
Mit dem Spatprodukt berechnet man das Volumen eines durch drei Vektoren aufgespannten Spats.
Die allgemeine Formel lautet: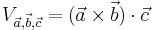 
Beispiel 1
Berechne das Volumen des Spat, das durch die Vektoren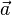 
=
, 
= 
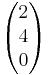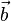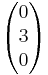und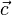 
= 
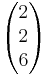aufgespannt wird.
Also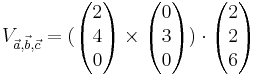 
= 
