Flächenberechnungen.: Unterschied zwischen den Versionen
Vieth1 (Diskussion | Beiträge) (→Kreis) |
(Kategorie:Differential- und Integralrechnung) |
||
| (8 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 59: | Zeile 59: | ||
;Formel: d= 2r | ;Formel: d= 2r | ||
: u= 2<math>\pi</math>r=<math> \pi</math>d | : u= 2<math>\pi</math>r=<math> \pi</math>d | ||
| − | : A=<math> \pi</math>r²= <math>\frac{ | + | : A=<math> \pi</math>r²= <math>\frac{\pi}{4} </math>d²[[Kategorie:Geometrie]]<br /> |
| + | <br /> | ||
| + | |||
| + | == Berechnung von Flächen durch Integrale == | ||
| + | Um die Größe eines Flächeninhalts auszurechen, muss zunächst einmal das Intervall der Funktion f(x) bestimmt werden. Wird beispielsweise die Fläche von der Funktion f(x) und der x- Achse eingeschlossen, so müssen erst die Nullstellen berechnet werden, wobei die Nullstellen gleichzeitig die Intervallgrenzen sind. <br /> | ||
| + | Bei der Integralrechnung können drei verschiedene Fälle eintreten.<br /> | ||
| + | Man kann den:<br /> | ||
| + | <br /> | ||
| + | 1. Flächeninhalt zwischen der Funktion f(x) und der x-Achse mit dem Intervall [a;b] berechen<br /> | ||
| + | 2. Flächeninhalt zwischen zwei Graphen ( f(x) und g(x) ) berechen<br /> | ||
| + | 3. Flächeninhalt mit dem Intavall <math>\lim_{x \to \infty}</math> bestimmen.<br /> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | 1. Funktion f(x)= ax²+bx+c Intervall[a;b] (a und b sind wie eben schon genannt, die Nullstellen)<br /> | ||
| + | <br /> | ||
| + | F(x)=<math>\int_{a}^{b} f(x)\, dx</math><br /> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | 2. Hier muss man zunächst die Schnittstellen von f(x) und g(x) bestimmen.<br /> | ||
| + | <br /> | ||
| + | F(x)=<math>\int_{a}^{b} f(x)\, dx</math><math>-</math><math>\ g(x)\, dx</math><br /> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | 3.F(x)= | ||
| + | |||
| + | |||
| + | |||
| + | [[Kategorie:Differential- und Integralrechnung]] | ||
Aktuelle Version vom 27. Dezember 2010, 10:31 Uhr
Inhaltsverzeichnis |
Rechteck
Die Diagonale sind gleich lang und halbieren einander.
Alle Innenwinkel sind gleich groß (90°).
Gegenüberliegende Seiten sind zueinander parallel und gleich lang.
- Formel
- u= 2(a+b)
- A= ab
Quadrat
Die Diagonalen sind zueinander senkrecht, gleich lang und halbierende einander.
Alle Innenwinkel sind gleich groß (90°).
Alles Seiten sind gleich lang.
- Formel
- u= 4a
- A= a²=
 c²
c²
Trapez
Mindestens zwei Seiten sind zueinander parallel.
- Formel
- u= a+b+c+d
- A= mh=
 (a+c)h
(a+c)h
Parallellogramm
Die Diagonale halbieren einander.
Gegenüberliegende Winkel sind gleich groß.
Gegenüberliegende Seiten sind zueinander parallel und gleich lang.
- Formel
- u= 2(a+b)
- A= aha= ab sin
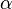
Drache
Die Diagonalen sind zueinander senkrecht.
Mindestens zwei gegenüberliegende Winkel sind gleich groß.
- Formel
- u= 2(a+c)
- A=
 ef
ef
Kreis
Der Mittelpunkt M hat zu allen Punkten auf der Kreislinie den gleichen Abstand.
Der Abstand vom Mittelpunkt M bis zur Kreislinie nennt man Radius r.
Der doppelte Radius ist gleichzeitig der Durchmesser.
- Formel
- d= 2r
- u= 2
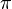 r=
r=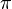 d
d
- A=
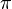 r²=
r²= 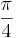 d²
d²
Berechnung von Flächen durch Integrale
Um die Größe eines Flächeninhalts auszurechen, muss zunächst einmal das Intervall der Funktion f(x) bestimmt werden. Wird beispielsweise die Fläche von der Funktion f(x) und der x- Achse eingeschlossen, so müssen erst die Nullstellen berechnet werden, wobei die Nullstellen gleichzeitig die Intervallgrenzen sind.
Bei der Integralrechnung können drei verschiedene Fälle eintreten.
Man kann den:
1. Flächeninhalt zwischen der Funktion f(x) und der x-Achse mit dem Intervall [a;b] berechen
2. Flächeninhalt zwischen zwei Graphen ( f(x) und g(x) ) berechen
3. Flächeninhalt mit dem Intavall 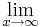 bestimmen.
bestimmen.
1. Funktion f(x)= ax²+bx+c Intervall[a;b] (a und b sind wie eben schon genannt, die Nullstellen)
F(x)=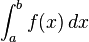
2. Hier muss man zunächst die Schnittstellen von f(x) und g(x) bestimmen.
F(x)=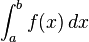

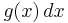
3.F(x)=

