Symmetrie.: Unterschied zwischen den Versionen
(→Beispiel 4) |
(→Beispiel 4) |
||
| Zeile 48: | Zeile 48: | ||
<br> | <br> | ||
Eine Termumformung liefert: <br> | Eine Termumformung liefert: <br> | ||
| − | <math>h_r=\frac { | + | <math>h_r=\frac {x*h_d}{o,5c}</math> fuer die Hoehe <math>h_r</math> |
| + | und <math>b=60-2x</math> fuer die grundseite b des Rechtecks | ||
<br>Wenn man diese ausnutzt ergibt sich die Funktion | <br>Wenn man diese ausnutzt ergibt sich die Funktion | ||
| − | <math>f( | + | <math>f(x)=\frac {x*h_d}{o,5c}*(60-2x)</math> <br> |
<math>h_d</math> ist in diesem Fall eine aus dem Satz des Pythagoras bekannte Größe: 40<br> | <math>h_d</math> ist in diesem Fall eine aus dem Satz des Pythagoras bekannte Größe: 40<br> | ||
Die vollkommen ausformulierte Funktionsformel lautet nun: | Die vollkommen ausformulierte Funktionsformel lautet nun: | ||
| − | <math>f( | + | <math>f(x)=\frac{4x^2}{3}-80x</math> |
<br> | <br> | ||
| − | <b>4. Ableiten. </b> <math>f'( | + | <b>4. Ableiten. </b> <math>f'(x)=\frac{8x}{3}-80</math> |
<br> | <br> | ||
<b>5. Extrempunkte bestimmen . </b> notwendige Bedingung fuer Extrema: f'(b)=0 | <b>5. Extrempunkte bestimmen . </b> notwendige Bedingung fuer Extrema: f'(b)=0 | ||
| + | <br> <math>0=\frac{8x}{3}-80</math> | ||
| + | <br> <math>80=\frac{8x}{3}</math> | ||
| + | <br> <math>30=x</math> | ||
| + | <br> | ||
<br> | <br> | ||
<b>6. Rand des Definitionsbereiches auf globale Extremstellen prüfen. </b> | <b>6. Rand des Definitionsbereiches auf globale Extremstellen prüfen. </b> | ||
| + | <math></math> | ||
Version vom 15. Februar 2011, 12:58 Uhr
Symmetrie beschreibt den Verlauf eines Graphen. Es gibt zwei verschiedene Symmetriearten. Einmal die Achsensymmetrie und zum anderen die Punktsymmetrie.
Die Achsensymmetrie spiegelt den Graphen auf der y-Achse.
Man geht folgendermaßen vor, um die y-Achsensymmetrie zu bestimmen:
f(-x)= f(x)
Hat man nun die Funktion f(x)=x4-4x2+10 gegeben, formt man die Funktion entsprechendermaßen nach f(-x)= f(x) um.
(-x)4 -4(-x)2+10 = x4-4x2+10
Nun kann man erkennen, dass f(-x) gleich f(x) ist und somit auch feststellen, dass es sich um eine Funktion handelt, die achsensymmetrisch ist.
Sind die Exponenten gerade kann man sagen, dass der Graph achsensymmetrisch sein muss.
Die Punktsymmetrie erkennt man dadurch, dass sie durch den Koordinaten-Ursprung verläuft.
Man geht folgendermaßen vor, um diese Symmetrie zu bestimmen.
f(-x)=-f(x)
Hat man die Funktion x5+x3+10, trägt man diese wieder in f(-x)=-f(x) ein. Sind beide Funktionsterme gleich, dann ist der Graph punktsymmetrisch.
-(x)5-(x)3+10 = - (x5+x3+10)
Sind die Exponenten ungerade kann man sagen, dass der Graph punktsymmetrisch ist.
Beispiel 4
Aufgabe: Aus einer Holzplatte, die die Form eines gleichschenkligen Dreiecks mit den Seiten a=50 cm, c=60cm hat, soll ein möglichst großes rechteckiges Brett herausgeschnitten werden.
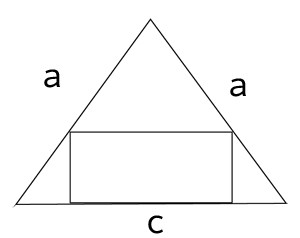
Wie groß kann das Rechteck höchstens sein, wenn die Basis b genannt wird und die Höhe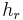
?
1. Zielfunktion aufstellen: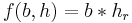 
2. Prüfen, ob Zielfunktion von Nebenbedingungen abhängt. Man kann in diesem Fall die Strahlensätze zur Findung einer Nebenbedingung ausnutzen, die uns eine Variable in abhaengigkeit der Anderen angibt.
3. Nebenbedingung suchen Die Höhe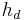 
des Dreiecks steht im Zusammenhang mit der Haelfte der Basis c, wie die Hoehe des Rechtecks 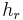zu dem Abschnitt x (zwischen der Basis des Rechtecks und dem Winkel) auf der Seite c 
:
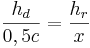
Eine Termumformung liefert:
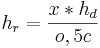fuer die Hoehe
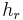und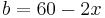 
fuer die grundseite b des Rechtecks
Wenn man diese ausnutzt ergibt sich die Funktion
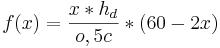
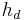ist in diesem Fall eine aus dem Satz des Pythagoras bekannte Größe: 40
Die vollkommen ausformulierte Funktionsformel lautet nun:
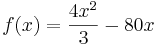
4. Ableiten.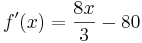 
5. Extrempunkte bestimmen . notwendige Bedingung fuer Extrema: f'(b)=0
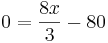
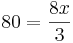
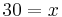
6. Rand des Definitionsbereiches auf globale Extremstellen prüfen.
