3.Abbau radioaktiver Substanzen im Körper: Unterschied zwischen den Versionen
| Zeile 19: | Zeile 19: | ||
<math>m(0)=c\cdot e^0=c=0,75</math> | <math>m(0)=c\cdot e^0=c=0,75</math> | ||
Mit der zweiten Angabe zusammen kann man c wieder in die Gleichung einsetzen und erhält: | Mit der zweiten Angabe zusammen kann man c wieder in die Gleichung einsetzen und erhält: | ||
| − | <math>m(2)=0,75\cdot e^{2\cdot a}=0,747 \gdw a= \ | + | <math>m(2)=0,75\cdot e^{2\cdot a}=0,747 \gdw a= \frac{1}{2}ln( \frac{747}{750}) \approx -0,0020 </math> |
Version vom 15. Februar 2011, 13:06 Uhr
Ein Kontrastmittel, das für Röntgenaufnahmen gespritzt wird, reichert sich in der Leber an. Dort wird es mit einer Rate abgebaut, die proportional zur vorhandenen Menge des Kontrastmittels belastet. Nach zwei Stunden lassen sich noch 0,747gr des Konstastmittels in der Leber nachweisen.
- A) Stellen sie eiene Differenzialgleichung für die Funktion m(t) auf, welche die Masse des Kontrastmittels in Abhängigkeit von der Zeit beschreibt, und lösen sie diese!
- B) Man kann das obige Modell verfeinern, indem man annimmt, dass das Kontrastmittel über ein gewissen Zeitraum hinweg gleichmäßig über den Blutstrom in die Leber gelangt.
Pro stunde werden 0,1gr zugeführt. Beschreiben sie diese Situation durch eine Differenzialgleichung und lösen sie diese.
- C) Als Kontastmittel wird das Radioaktiveelement Jod 131 verwendet, das eine Halbwertszeit von 8 Tagen besitzt. Bestimmen sie die Zerfallskonstante.
- D) Zum Zeitpunkt t=0 ist genau 1mg Jod nachweisbar,nach einer gewissen Zeit sind es noch 0,298mg. Wie viel Zeit ist zwischen den Messungen vergangen?
- E)In einem anfangs leerem Gefäß,gelangen gleichmäßig 0,1 mg Jod pro Stunde. Wie viel jod befindet sich nach, 2 Wochen im Gefäß?
Lösungen:
- A) Sei m(t) die Funktion, die die Masse des Konstrastmittels zum Zeitpunkt t beschreibt und a die Abbaurate.
Da nach Voraussetzung die Abbaurate proportional zur Masse ist, gilt also:
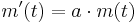mit der Lösung: 
,
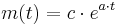wobei c eine beliebige reelle Konstante und a eine negative reele Zahl ist, da es sich um eine Abbaurate handelt.
Laut Aufgabenstellung gilt dann:
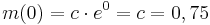Mit der zweiten Angabe zusammen kann man c wieder in die Gleichung einsetzen und erhält:
Fehler beim Parsen(Unbekannte Funktion „\gdw“): m(2)=0,75\cdot e^{2\cdot a}=0,747 \gdw a= \frac{1}{2}ln( \frac{747}{750}) \approx -0,0020
