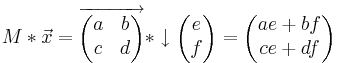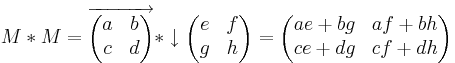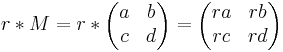Affine Abbildungen und deren Eigenschaften.: Unterschied zwischen den Versionen

Aus KAS-Wiki
Wechseln zu: Navigation, Suche
Zeile 2: Zeile 2:
  
  
−
== '''''Definition''''' ==
+
== Definition ==
  
  
Zeile 9: Zeile 9:
 
   
 
   
 
    
 
    
−
== '''''Matrizenrechnung''''' ==
+
== Matrizenrechnung ==
 
   
 
   
  

Version vom 8. Dezember 2009, 12:08 Uhr

Affine Abbildungen


Definition

Affine Abbildungen sind geometrische Projektionen. Mit Hilfe von Abbildungsmatrizen wird ein geometrischer Prozess wie z.B. Spiegelungen, Drehungen um beliebige Zentren, Streckungen oder Stauchungen mathematisch erfasst und beschrieben. Um mit ihnen umgehen zu können bedarf es der Rechenregeln für Matrizen.


Matrizenrechnung

Affine Abbildungen werden im zweidimensionelem Raum durch 2X2 Matrizen ausgedrückt. Sie haben die Form 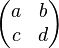\begin{pmatrix} a & b \\ c & d \end{pmatrix}. Für die affinen Abbildungen wichtige Rechenoperationen sind vor allem die Multiplikationen. Dabei gelten folgende Regeln:

M*\vec x=\overrightarrow\begin{pmatrix} a & b \\ c & d \end{pmatrix}*\downarrow\begin{pmatrix} e \\ f \end{pmatrix}=\begin{pmatrix} ae+bf \\ ce+df \end{pmatrix}

M*M=\overrightarrow\begin{pmatrix} a & b \\ c & d \end{pmatrix}*\downarrow\begin{pmatrix} e & f \\ g & h \end{pmatrix}=\begin{pmatrix} ae+bg & af+bh \\ ce+dg & cf+dh \end{pmatrix}

r*M=r*\begin{pmatrix} a & b \\ c & d \end{pmatrix}=\begin{pmatrix} ra & rb \\ rc & rd \end{pmatrix}

Von „http://kas.zum.de/index.php?title=Affine_Abbildungen_und_deren_Eigenschaften.&oldid=553“