Auswertung: Unterschied zwischen den Versionen
Aus KAS-Wiki
Belgin (Diskussion | Beiträge) |
Belgin (Diskussion | Beiträge) |
||
| Zeile 2: | Zeile 2: | ||
== Auswertung == | == Auswertung == | ||
| − | <br /><br />Wir betrachten die drei Bewegungen des Messwagens jeweils von der Fahrbahnmarke<br /> 0 aus und lassen die Zeitrechnung bei null beginnen, wenn die vordere Kante des Messaufsatzes die Fahrbahnmarke 0 passiert.<br /> Nach der Zeit <math>\delta</math>t1 hat sie dann dieOrtskoordinate 1,0 ( Durchmesser der Messaufsatzes),<br /> nach der Zeit <math>\delta</math>t die Ortskoordinate 20,0 und nach der Zeit <math>\delta</math>t+<math>\delta</math>t2 die Ortskoordinate 21,0. | + | <br /><br />Wir betrachten die drei Bewegungen des Messwagens jeweils von der Fahrbahnmarke<br /> 0 aus und lassen die Zeitrechnung bei null beginnen, wenn die vordere Kante des Messaufsatzes die Fahrbahnmarke 0 passiert.<br /> Nach der Zeit <math>\delta</math>t1 hat sie dann dieOrtskoordinate 1,0 ( Durchmesser der Messaufsatzes),<br /> nach der Zeit <math>\delta</math>t die Ortskoordinate 20,0 und nach der Zeit <math>\delta</math>t+<math>\delta</math>t2 die Ortskoordinate 21,0.<br /><br /> |
| + | (1) Trage die Messwerte für die 2. Bewegung in ein x-t- Diagramm ein und verbinde sie zu einem sinnvollen Graph.<br /> Wähle hierzu günstige Einheiten, vor allem für die Zeitachse, um auch die Graphen für die beiden anderen<br /> Bewegungen vollständig aufnehmen können. | ||
Version vom 22. Juni 2011, 08:57 Uhr
Auswertung
Wir betrachten die drei Bewegungen des Messwagens jeweils von der Fahrbahnmarke
0 aus und lassen die Zeitrechnung bei null beginnen, wenn die vordere Kante des Messaufsatzes die Fahrbahnmarke 0 passiert.
Nach der Zeit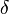 
t1 hat sie dann dieOrtskoordinate 1,0 ( Durchmesser der Messaufsatzes),
nach der Zeit 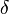t die Ortskoordinate 20,0 und nach der Zei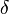t t+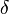t2 die Ortskoordinate 21,0.
(1) Trage die Messwerte für die 2. Bewegung in ein x-t- Diagramm ein und verbinde sie zu einem sinnvollen Graph.
Wähle hierzu günstige Einheiten, vor allem für die Zeitachse, um auch die Graphen für die beiden anderen
Bewegungen vollständig aufnehmen können.
