Darstellung von Geraden und Ebenen.: Unterschied zwischen den Versionen
| Zeile 24: | Zeile 24: | ||
Bei einer Ebene handelt es sich um ein unbegrenzt ausgedehntes flaches zweidimensionales Objekt. | Bei einer Ebene handelt es sich um ein unbegrenzt ausgedehntes flaches zweidimensionales Objekt. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
=== Gegenseite Lage von Ebenen === | === Gegenseite Lage von Ebenen === | ||
| Zeile 57: | Zeile 52: | ||
Bei n1, n2 und n3 handelt es sich um die Koordinaten eines zur Ebene gehörenden Normalenvektors <math>\vec n</math>. | Bei n1, n2 und n3 handelt es sich um die Koordinaten eines zur Ebene gehörenden Normalenvektors <math>\vec n</math>. | ||
| + | |||
| + | === Parameter === | ||
| + | |||
| + | Die Parameterform lässt sich durch eine Gleichung der Form: | ||
| + | <math>\vec x = \vec p + r \cdot \vec u + s \cdot \vec v</math> beschreiben. | ||
| + | |||
| + | Hierbei ist <math>\vec p</math> ein Stützvektor un die linear unabhänigen Vektoreb <math>\vec u</math> und <math>\vec v</math> sind zwei Spannvektoren. | ||
Version vom 14. Dezember 2009, 11:10 Uhr
Inhaltsverzeichnis |
Geraden
Eine Gerade ist eine unendlich lange und unendlich dünne Linie. Sie besitzt keine Eigenschaften, es besteht lediglich die Beziehung zu anderen Geraden, Punkten und Ebenen, die von Bedeutung sind.
Jede Gerade lässt sich durch eine Gleichung der Form:
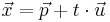beschreiben.
Die Gerade wird in der Parameterdarstellung beschrieben, indem ein Ortsvektor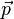 
auf einen beliebigen Punkt der Gerade gerichtet wird und zudem von diesem Punkt ein Richtungsvektor 
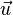den Verlauf der Geraden bestimmt.
Gegenseitige Lage von Geraden
Zwei Geraden können folgende Lagebeziehungen zueinander haben. Sie können:
- identisch sein: Beide Geraden haben alle Punkte gemeinsam. (Die Vektorengleichung hat unendlich viele Lösungen.)
- sich schneiden: Beide Geraden haben genau einen Punkt gemeinsam. (Die Vektorengleichung hat genau eine Lösung.) (linear unabhängig)
- zueinander parallel sein: Beide Geraden haben keinen Punkt gemeinsam und lassen sich durch eine Verschiebung ineinander überführen. (linear abhängig)
- zueinander windschief sein: Beide Geraden haben keinen Punkt gemeinsam, aber lassen sich nicht durch eine Verschiebung allein ineinander überführen. (linear unabhängig)
- keine gemeinsamen Punkte haben: Beide Geraden haben keine Punkte gemeinsam. (Die Vektorengleichung hat keine Lösung.)
Ebenen
Bei einer Ebene handelt es sich um ein unbegrenzt ausgedehntes flaches zweidimensionales Objekt.
Gegenseite Lage von Ebenen
Zwei Ebenen können folgende Lagebeziehungen zueinander haben. Sie können:
- sich schneiden: Beide Ebenen schneiden sich in einer Geraden. (Die Gleichung hat unendlich viele Lösungen.) (linear unabhängig)
- zueinander parallel sein: Beide Ebenen haben keine gemeinsamen Punkte. (Die Gleichung hat keine Lösung.) (linear abhängig)
- keine gemeinsamen Punkte haben
Normalgleichung
Die Normalgleichung einer Ebene hat die Form: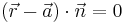 
Wobei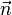 
ein Normalenvektor der Ebene, 
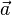der Ortsvektor eines beliebigen Punktes ist, der in der Ebene liegt und 
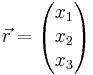der Vektor der Unbekannten ist.
Der Operator 
steht für das Skalarprodukt.
Die Normalform ist eine Gleichung, die eine Ebene im dreidemensinalen Raum oder eine Gerade im zweidemensionalen Raum. Sie wird hauptsächlich für Abstandsberechnungen verwendet. In vektorieller Schreibweise lautet sie: 
Koordinatenform
Die Koordinatenform ist eine Form der Ebenengleichung im Raum.
Sie sieht folgendermaßen aus: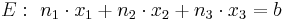 
.
Hierbei sind x1, x2 und x3 die Koordinaten im Raum, b ist eine reelle Zahl.
Bei n1, n2 und n3 handelt es sich um die Koordinaten eines zur Ebene gehörenden Normalenvektors .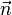
Parameter
Die Parameterform lässt sich durch eine Gleichung der Form:
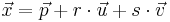beschreiben.
Hierbei ist 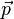ein Stützvektor un die linear unabhänigen Vektoreb 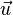und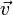 
sind zwei Spannvektoren.
