Das Orbitalmodell: Unterschied zwischen den Versionen
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) | |||
| Zeile 4: | Zeile 4: | ||
Weiterhin besagt die '''Heisenbergsche Unschärferelation''', dass es aufgrund der hohen Geschwindigkeiten und den geringen Massen von Elektronen unmöglich ist Geschwindigkeit und Position eines Elektrons gleichzeitig zu messen, da das Elektron durch die Messung abgelenkt wird. | Weiterhin besagt die '''Heisenbergsche Unschärferelation''', dass es aufgrund der hohen Geschwindigkeiten und den geringen Massen von Elektronen unmöglich ist Geschwindigkeit und Position eines Elektrons gleichzeitig zu messen, da das Elektron durch die Messung abgelenkt wird. | ||
| − | Pro Periode im Periodensystem gibt es einen weiteren Typ an Orbitalen, so gibt es in der ersten Periode nur das 1s-Orbital, welches zwei Elektronen aufnhemen kann. Das Wasserstoff-Atom hat nur ein Elektron, dieses bewegt sich um den Kern herum, also hat das s-Orbital immer ein Kugel-Form. Dazu wird die Anzahl der in dem Orbital vorhandenen Elektronen angegeben, also entspricht Wasserstoff 1s<sup>1</sup> und Helium 1s<sup>2</sup>.<br /> | + | Pro Periode im Periodensystem gibt es einen weiteren Typ an Orbitalen, so gibt es in der ersten Periode nur das 1s-Orbital, welches zwei Elektronen aufnhemen kann. Das Wasserstoff-Atom hat nur ein Elektron, dieses bewegt sich um den Kern herum, also hat das s-Orbital immer ein Kugel-Form. Dazu wird die Anzahl der in dem Orbital vorhandenen Elektronen angegeben, also entspricht Wasserstoff 1s<sup>1</sup> und [[Helium]] 1s<sup>2</sup>.<br /> |
In der zweiten Periode gibt es nun das 2s-Orbital, welches um das 1s-Orbital herum liegt und eine Knotenebene bildet sich zwischen den beiden Orbitalen aus, in der die Aufenthaltswahrscheinlich null beträgt. Hinzu kommen die 2p-Orbitale, welche eine "Lappen-" oder "Hantel-Form" aufweisen und in einem Koordinatensytsem auf den Achsen liegen würden, also orthogonal zueinander sind. Am Schnittpunkt der beiden Lappen liegt die Aufenthaltswahrscheinlichkeit bei null. Jedes dieser Orbitale kann ebenfalls zwei Elektronen aufnehmen, so kommen bei gefüllten Orbitalen sechs Elektronen in den 2p-Orbitalen, zwei in dem 2s- und zwei in dem 1s-Orbital zusammen, also ergibt sich mit 10 Elektronen eine Edelgaskonfiguration.<br /> | In der zweiten Periode gibt es nun das 2s-Orbital, welches um das 1s-Orbital herum liegt und eine Knotenebene bildet sich zwischen den beiden Orbitalen aus, in der die Aufenthaltswahrscheinlich null beträgt. Hinzu kommen die 2p-Orbitale, welche eine "Lappen-" oder "Hantel-Form" aufweisen und in einem Koordinatensytsem auf den Achsen liegen würden, also orthogonal zueinander sind. Am Schnittpunkt der beiden Lappen liegt die Aufenthaltswahrscheinlichkeit bei null. Jedes dieser Orbitale kann ebenfalls zwei Elektronen aufnehmen, so kommen bei gefüllten Orbitalen sechs Elektronen in den 2p-Orbitalen, zwei in dem 2s- und zwei in dem 1s-Orbital zusammen, also ergibt sich mit 10 Elektronen eine Edelgaskonfiguration.<br /> | ||
In den weiteren Perioden kommen noch die d- und die f-Orbitale hinzu mit einer maximalen Kapazität von zehn bzw. 14 Elektronen. | In den weiteren Perioden kommen noch die d- und die f-Orbitale hinzu mit einer maximalen Kapazität von zehn bzw. 14 Elektronen. | ||
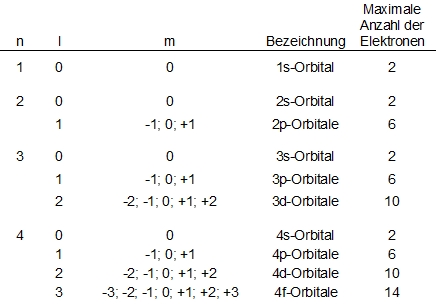
Jedes Orbital lässt sich durch einen Satz aus drei Quantenzahlen definieren: Die '''Hauptquantenzahl n''' bezeichnet die Periode und nimmt die Werte von 1 bis 7 an. Die '''Nebenquantenzahl l''' untergliedert die Orbitale einer Periode in Klassen von Orbitalen verschiedener Energien und Formen und nimmt Werte von 0 bis n-1 an. Die '''magnetische Quantenzahl m''' gibt das Verhalten eines Elektrons im magnetischen Feld an und nimmt Werte von -l bis l an. Somit lässt sich erklären, dass es ein s-Orbital, drei p-Orbitale, fünf d-Orbitale und sieben f-Orbitale gibt.<br /> | Jedes Orbital lässt sich durch einen Satz aus drei Quantenzahlen definieren: Die '''Hauptquantenzahl n''' bezeichnet die Periode und nimmt die Werte von 1 bis 7 an. Die '''Nebenquantenzahl l''' untergliedert die Orbitale einer Periode in Klassen von Orbitalen verschiedener Energien und Formen und nimmt Werte von 0 bis n-1 an. Die '''magnetische Quantenzahl m''' gibt das Verhalten eines Elektrons im magnetischen Feld an und nimmt Werte von -l bis l an. Somit lässt sich erklären, dass es ein s-Orbital, drei p-Orbitale, fünf d-Orbitale und sieben f-Orbitale gibt.<br /> | ||
| − | Die Orbitale werden in unterschiedlicher Reihenfolge aufgefüllt, je nach dem wie hoch das Energie-Niveau ist. So wird z.B. das 4s-Orbital vor den 3d-Orbitalen gefüllt. Dabei wird ein Orbital zunächst nur mit einem Elektron gefüllt, erst wenn als anderen Orbitale des selben Energieniveaus auch ein Elektron erhalten wird ein zweites eingesetzt ('''Hundsche Regel'''). Nach dem '''Pauli-Prinzip''' müssen Elektronen sich in ihren Eigeschaften unterscheiden, das heißt, wenn die ersten drei Quantenzahlen von zwei Elektronen gleich sind, ist die '''Spinquantenzahl s''' von Bedeutung. Sie gibt den spin eines Elektrons und beträgt nur -<sup>1</sup>/<sub>2</sub> oder +<sup>1</sup>/<sub>2</sub>. | + | Die Orbitale werden in unterschiedlicher Reihenfolge aufgefüllt, je nach dem wie hoch das Energie-Niveau ist. So wird z.B. das 4s-Orbital vor den 3d-Orbitalen gefüllt. Dabei wird ein Orbital zunächst nur mit einem Elektron gefüllt, erst wenn als anderen Orbitale des selben Energieniveaus auch ein Elektron erhalten wird ein zweites eingesetzt ('''Hundsche Regel'''). Nach dem '''Pauli-Prinzip''' müssen Elektronen sich in ihren Eigeschaften unterscheiden, das heißt, wenn die ersten drei Quantenzahlen von zwei Elektronen gleich sind, ist die '''Spinquantenzahl s''' von Bedeutung. Sie gibt den spin eines Elektrons und beträgt nur -<sup>1</sup>/<sub>2</sub> oder +<sup>1</sup>/<sub>2</sub>. |
| + | |||
| + | |||
| + | |||
| + | |||
[[Bild:orbital-tabelle.jpg]][[Bild:energieniveau.png]] | [[Bild:orbital-tabelle.jpg]][[Bild:energieniveau.png]] | ||
Aktuelle Version vom 5. Juli 2011, 15:15 Uhr
Das Orbitalmodell ist ein chemisches Modell von Atomen, welches von verschiedenen Wissenschaftlern entwickelt wurde und auf der Quantenphysik beruht. Mit ihm lassen sich viele bis dahin unerklärliche chemische Phänomene begründen.
Die wichtigste Vorraussetzung für das Orbitalmodell ist der Welle-Teilchen-Dualismus (de-Broglie-Beziehung), welcher besagt, dass Elektronen Eigenschaften von Wellen, aber auch von Teilchen annehmen können. So kann man die Schrödinger-Gleichung aufstellen, durch die man die Aufenthaltswahrscheinlich eines Elektrons ermitteln kann, denn diese befinden sich im Gegensatz zum Bohrschen Atommodell nicht auf festgelegten Bahnen (Trajektorien). Dauraus ergibt sich, dass das ein Orbital den Raum umschließt, in dem sich ein Elektron mit 90 prozentiger Wahrscheinlichkeit aufhält. Es kann als "Unterschale" einer Schale im Bohrschen Atommodell gesehen werden.
Weiterhin besagt die Heisenbergsche Unschärferelation, dass es aufgrund der hohen Geschwindigkeiten und den geringen Massen von Elektronen unmöglich ist Geschwindigkeit und Position eines Elektrons gleichzeitig zu messen, da das Elektron durch die Messung abgelenkt wird.
Pro Periode im Periodensystem gibt es einen weiteren Typ an Orbitalen, so gibt es in der ersten Periode nur das 1s-Orbital, welches zwei Elektronen aufnhemen kann. Das Wasserstoff-Atom hat nur ein Elektron, dieses bewegt sich um den Kern herum, also hat das s-Orbital immer ein Kugel-Form. Dazu wird die Anzahl der in dem Orbital vorhandenen Elektronen angegeben, also entspricht Wasserstoff 1s1 und Helium 1s2.
In der zweiten Periode gibt es nun das 2s-Orbital, welches um das 1s-Orbital herum liegt und eine Knotenebene bildet sich zwischen den beiden Orbitalen aus, in der die Aufenthaltswahrscheinlich null beträgt. Hinzu kommen die 2p-Orbitale, welche eine "Lappen-" oder "Hantel-Form" aufweisen und in einem Koordinatensytsem auf den Achsen liegen würden, also orthogonal zueinander sind. Am Schnittpunkt der beiden Lappen liegt die Aufenthaltswahrscheinlichkeit bei null. Jedes dieser Orbitale kann ebenfalls zwei Elektronen aufnehmen, so kommen bei gefüllten Orbitalen sechs Elektronen in den 2p-Orbitalen, zwei in dem 2s- und zwei in dem 1s-Orbital zusammen, also ergibt sich mit 10 Elektronen eine Edelgaskonfiguration.
In den weiteren Perioden kommen noch die d- und die f-Orbitale hinzu mit einer maximalen Kapazität von zehn bzw. 14 Elektronen.
Jedes Orbital lässt sich durch einen Satz aus drei Quantenzahlen definieren: Die Hauptquantenzahl n bezeichnet die Periode und nimmt die Werte von 1 bis 7 an. Die Nebenquantenzahl l untergliedert die Orbitale einer Periode in Klassen von Orbitalen verschiedener Energien und Formen und nimmt Werte von 0 bis n-1 an. Die magnetische Quantenzahl m gibt das Verhalten eines Elektrons im magnetischen Feld an und nimmt Werte von -l bis l an. Somit lässt sich erklären, dass es ein s-Orbital, drei p-Orbitale, fünf d-Orbitale und sieben f-Orbitale gibt.
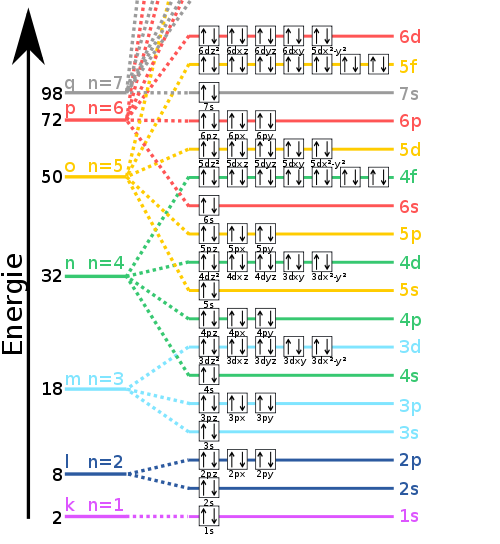
Die Orbitale werden in unterschiedlicher Reihenfolge aufgefüllt, je nach dem wie hoch das Energie-Niveau ist. So wird z.B. das 4s-Orbital vor den 3d-Orbitalen gefüllt. Dabei wird ein Orbital zunächst nur mit einem Elektron gefüllt, erst wenn als anderen Orbitale des selben Energieniveaus auch ein Elektron erhalten wird ein zweites eingesetzt (Hundsche Regel). Nach dem Pauli-Prinzip müssen Elektronen sich in ihren Eigeschaften unterscheiden, das heißt, wenn die ersten drei Quantenzahlen von zwei Elektronen gleich sind, ist die Spinquantenzahl s von Bedeutung. Sie gibt den spin eines Elektrons und beträgt nur -1/2 oder +1/2.