Nernst-Gleichung: Unterschied zwischen den Versionen
(→Spezialfälle der Nernst-Gleichung) |
|||
| Zeile 65: | Zeile 65: | ||
<math> H_{2}(g) + 2 H_{2}O \rightarrow2H_{3}O^{+}(aq) + 2e^{-}</math> | <math> H_{2}(g) + 2 H_{2}O \rightarrow2H_{3}O^{+}(aq) + 2e^{-}</math> | ||
<br /> | <br /> | ||
| + | <br /> | ||
| + | und dem Standardelektrodenpotential <math>E^\circ = 0</math>, so vereinfacht sich die Nernst-Gleichung wie folgt: <br /> | ||
<br /> | <br /> | ||
Version vom 14. Dezember 2009, 18:41 Uhr
Die Nernst-Gleichung beschreibt den Einfluss der Konzentration auf das Potential eines Redoxsystems.
Allgemein lässt sich die Nernst-Gleichung wie folgt formulieren:
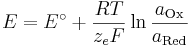
Unter Standardbedingungen vereinfacht sich die Nernst-Gleichung und man betrachtet nur noch die Abhängigkeit von der Konzentration.
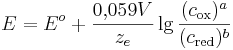
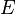Elektrodenpotential
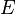° Standardelektronenpotential
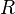molare Gaskonstante
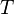Temperatur in Kelvin
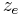Anzahl der übertragenen Elektronen
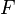Faraday-Konstante
Herleitung der Nernst-Gleichung
Am Beispiel einer Konzentrationszelle aus einer Standard-Silber-Halbzelle und einer Silberhalbzelle mit unterschiedlichen Konzentrationen lässt sich die Nernst-Gleichung in einfacher Form ableiten.
Variiert man nämlich die Konzentration der Nicht-Standard-Silberzelle und misst die resultierende Spannung, kann man die Messreihe mit Hilfe der Logarithmus-Funktion linearisieren:
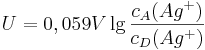
wobei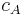 
die Konzentration in der Donator-Halbzelle angibt und 
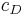die Konzentration in der Donator-Halbzelle.
Unser Ziel ist es aber, die Spannung in einer einzelnen Zelle bestimmen zu können. Dazu macht man sich am besten klar, dass die Zellspannung die Differenz der einzelnen Elektroden-Potentiale der Halbzellen ist:
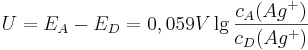
Unter der Annahme, dass es sich bei der Akzeptor-Halbzelle um eine Standard-Halbzelle handelt und somit auch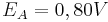 
ist, kann man die Gleichung weiter vereinfachen:
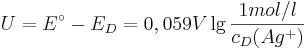
Was nach umformen folgende Gleichung liefert:
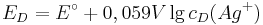
Hiermit lässt sich nun das Elektroden-Potential einer beliebigen Silberhalbzelle berechnen. Die allgemeine Nernst-Gleichung selbst lässt sich aber nur auf thermodynamischem Wege herleiten.
Spezialfälle der Nernst-Gleichung
Betrachtet man zunächst das Redoxpaar Wasserstoff/Oxonium-Ion mit der Redoxgleichung
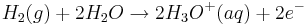
und dem Standardelektrodenpotential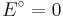 
, so vereinfacht sich die Nernst-Gleichung wie folgt:
