Nernst-Gleichung: Unterschied zwischen den Versionen
(→Wasserstoff-Halbzellen) |
(→Wasserstoff-Halbzellen) |
||
| Zeile 72: | Zeile 72: | ||
<br /> | <br /> | ||
<math>E = 0 + \frac{0{,}059 V}{2}\lg{(c^{2}(H_{3}O^{+})} = 0,059 V \lg c(H_{3}O^{+}) = -0,059 V pH </math> <br /> | <math>E = 0 + \frac{0{,}059 V}{2}\lg{(c^{2}(H_{3}O^{+})} = 0,059 V \lg c(H_{3}O^{+}) = -0,059 V pH </math> <br /> | ||
| − | Denn der pH-Wert ist definiert als <math>-\ | + | <br /> |
| + | Denn der pH-Wert ist definiert als <math>-\lg {c( H_{3}O^{+})}^{ }_{ }</math> . | ||
<br /> | <br /> | ||
<br /> | <br /> | ||
Aktuelle Version vom 17. Dezember 2009, 11:57 Uhr
Die Nernst-Gleichung beschreibt den Einfluss der Konzentration auf das Potential eines Redoxsystems.
Allgemein lässt sich die Nernst-Gleichung wie folgt formulieren:
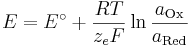
Unter Standardbedingungen vereinfacht sich die Nernst-Gleichung und man betrachtet nur noch die Abhängigkeit von der Konzentration.
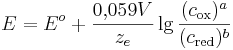
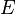 Elektrodenpotential
Elektrodenpotential
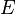 ° Standardelektronenpotential
° Standardelektronenpotential
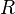 molare Gaskonstante
molare Gaskonstante
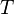 Temperatur in Kelvin
Temperatur in Kelvin
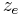 Anzahl der übertragenen Elektronen
Anzahl der übertragenen Elektronen
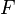 Faraday-Konstante
Faraday-Konstante
Inhaltsverzeichnis[Verbergen] |
Herleitung der Nernst-Gleichung
Am Beispiel einer Konzentrationszelle aus einer Standard-Silber-Halbzelle[1] und einer Silberhalbzelle mit unterschiedlichen Konzentrationen lässt sich die Nernst-Gleichung in einfacher Form ableiten.
Variiert man nämlich die Konzentration der Nicht-Standard-Silberzelle und misst die resultierende Spannung, kann man die Messreihe mit Hilfe der Logarithmus-Funktion linearisieren:
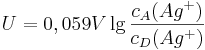
wobei 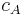 die Konzentration in der Donator-Halbzelle angibt und
die Konzentration in der Donator-Halbzelle angibt und 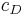 die Konzentration in der Donator-Halbzelle.
Unser Ziel ist es aber, die Spannung in einer einzelnen Zelle bestimmen zu können. Dazu macht man sich am besten klar, dass die Zellspannung die Differenz der einzelnen Elektroden-Potentiale (Quantitative Redoxreihe) der Halbzellen ist:
die Konzentration in der Donator-Halbzelle.
Unser Ziel ist es aber, die Spannung in einer einzelnen Zelle bestimmen zu können. Dazu macht man sich am besten klar, dass die Zellspannung die Differenz der einzelnen Elektroden-Potentiale (Quantitative Redoxreihe) der Halbzellen ist:
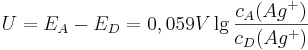
Unter der Annahme, dass es sich bei der Akzeptor-Halbzelle um eine Standard-Halbzelle handelt und somit auch 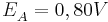 ist, kann man die Gleichung weiter vereinfachen:
ist, kann man die Gleichung weiter vereinfachen:
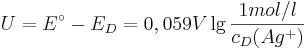
Was nach umformen folgende Gleichung liefert:
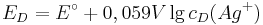
Hiermit lässt sich nun das Elektroden-Potential einer beliebigen Silberhalbzelle berechnen. Die allgemeine Nernst-Gleichung selbst lässt sich aber nur auf thermodynamischem Wege herleiten.
Spezialfälle der Nernst-Gleichung
Wasserstoff-Halbzellen
Betrachtet man zunächst das Redoxpaar Wasserstoff/Oxonium-Ion (Standardwasserstoffhalbzelle) mit der Redoxgleichung
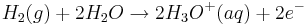
und dem Standardelektrodenpotential 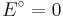 , so vereinfacht sich die Nernst-Gleichung wie folgt:
, so vereinfacht sich die Nernst-Gleichung wie folgt:
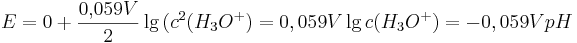
Denn der pH-Wert ist definiert als 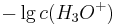 .
.
Gleichgewichtskonstanten
Man kann die Nernst-Gleichung auch umformen und damit die Gleichgewichtskonstante K von reversiblen Redoxreaktionen ermitteln. Die genaue Herleitung wird an dieser Stelle jedoch ausgespart:
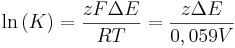
Dieses Ergebnis ist auch sinnvoll, da im Gleichgewicht keine Spannung mehr messbar ist, da kein Konzentrations- bzw. Potentialgefälle (Elektrische Doppelschicht) mehr vorhanden ist, das als Triebkraft für die Redoxreaktionen dienen könnte. Ist die Spannung der Zelle also auf 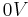 abgesunken, so hat sich das chemische Gleichgewicht eingestellt.
abgesunken, so hat sich das chemische Gleichgewicht eingestellt.
Literaturverzeichnis
Tausch, Michael: Chemie SII. Stoff - Formel - Umwelt, Aus: C.C.Buchner, Bamberg 2008, S. 183-188

