Krahn 2 AACP: Unterschied zwischen den Versionen
Sarah8 (Diskussion | Beiträge) |
|||
| (24 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
== '''Konzept zum Kranbau von Asena, Angelina, Clara & Priska''' == | == '''Konzept zum Kranbau von Asena, Angelina, Clara & Priska''' == | ||
| − | '''''Materialien | + | '''Aufgabe:'''Die Aufgabe war es, einen Kran zu konstruieren, er ein stabiles Gerüst hat. Bevor wir mit unsere Planung anfingen, haben wir viele Versuche zu Kraftausgleich und Kraft im Allgemeinen gemacht. Die Gruppe, die mit ihrem Schätzungsergebnis, wie viel der Kran tragen kann, am nähesten liegt hat gewonnen. |
| + | |||
| + | |||
| + | == '''''Materialien''''' == | ||
| + | |||
* kurze, dickere Strohalme ohne Knick | * kurze, dickere Strohalme ohne Knick | ||
* Strohalme mit Knick | * Strohalme mit Knick | ||
| Zeile 9: | Zeile 13: | ||
* Heißklebepistole | * Heißklebepistole | ||
| − | '''Inspiration | + | =='''Inspiration'''== |
| − | [[Bild:Crane.jpg | 353px ]] | + | [[Bild:Crane.jpg | 353px ]] |
| + | |||
| + | |||
| + | == '''Skizze Vorderseite'''== | ||
| − | |||
<gallery> | <gallery> | ||
| Zeile 19: | Zeile 25: | ||
</gallery> | </gallery> | ||
| − | Wir haben uns überlegt, dass sich die Strohhalme kreuzen, damit sich die Kräfte gegeseitig aufheben. Dies geschieht, weil die Kräfte, einmal die nach unten drücken und die nach oben drücken, gegeneinander wirken. Dadurch werden sie aufgehoben | + | [[Bild:Kran_1234567890.jpg | 400 px ]] |
| + | |||
| + | |||
| + | == '''Konstruktion''' == | ||
| + | |||
| + | |||
| + | Der Kran ist rechteckig, anstatt von quadratischer Form. Wir haben, für jeweils eine Seite des Bausteins des unteren Teils zwei kleine Konstruktionen erstellt: 1 Loch in die Mitte eines langen, dicken Strohhalmes gebohrt und einen anderen dicken Strohhalm dadurch gesteckt, sozusagen eine X-Form erstellt. Diese 2 Strohhalm-Konstruktionen "X" haben wir miteinander verbunden und dann oben | ||
| + | |||
| + | Wir haben uns überlegt, dass sich die Strohhalme kreuzen, damit sich die Kräfte gegeseitig aufheben. Dies geschieht, weil die Kräfte, einmal die nach unten drücken und die, die nach oben drücken ( in der Zeichnung mit Pfeilen dargestellt), gegeneinander wirken ( das kann man in der Skizze anhand der Pfeile die gegeneinander zeigen sehen ). Dadurch werden sie aufgehoben und die einzelnen Stockwerke des Krans brechen nicht zusammen. Das ist wie wenn man seine Hände zusammen drückt, dabei werden auch die Kräfte aufgehoben, sodass die Hände nicht zur einen Seite gedrückt werden, sondern in der Mitte bleiben. Die Kräfte werden allerdings nur aufgehoben, wenn beide wirkenden Kräfte die gleiche Stärke haben, wenn das nicht der Fall ist, wird die eine Seite, von der die schwächere Kraft aus wirkt, weggedrückt, weil die andere Kraft stärker ist. | ||
| + | |||
| + | |||
| + | == '''''Rechnung zur Tragekraft des später fertigen Krans''' == | ||
| − | |||
'' | '' | ||
70cm lang ist der Fuß des Krans, 50cm der Tragarm. | 70cm lang ist der Fuß des Krans, 50cm der Tragarm. | ||
| − | '''F1:''' 10N | + | '''F1 (Lastarm 1-Kraft):''' 10N |
| − | '''F2:''' ? | + | '''F2(Lastarm 2-Kraft):''' ? |
| − | '''r<sub>1</sub>:''' 50cm | + | '''r<sub>1</sub>(Länge der Lastarme):''' 50cm |
'''r<sub>2</sub>:''' 40 cm | '''r<sub>2</sub>:''' 40 cm | ||
| − | -> Um das Ergebnis rauszubekommen, wie viel F2 tragen kann, haben wir die Länge und Kraft des | + | -> Um das Ergebnis rauszubekommen, wie viel F2 tragen kann, haben wir die Länge und Kraft des Lastarms gefunden. |
| − | '' | + | ''Formel'': F1 * r<sub>1</sub>=F2*r<sub>2</sub> |
| − | 10N*50cm=F2*40cm | + | ''Einsetzen der Längen:'' 10N*50cm=F2*40cm |
'''F2''' = 10*50/40 = 500/40 | '''F2''' = 10*50/40 = 500/40 | ||
| Zeile 41: | Zeile 57: | ||
''Ergebnis:'' '''F2=12,5N''' | ''Ergebnis:'' '''F2=12,5N''' | ||
| − | Somit kann unser Kran eine Kraft von 12,5 Newton tragen! | + | Somit kann unser Kran eine Kraft von '''12,5''' Newton tragen! |
Aktuelle Version vom 2. Februar 2012, 15:10 Uhr
Inhaltsverzeichnis |
Konzept zum Kranbau von Asena, Angelina, Clara & Priska
Aufgabe:Die Aufgabe war es, einen Kran zu konstruieren, er ein stabiles Gerüst hat. Bevor wir mit unsere Planung anfingen, haben wir viele Versuche zu Kraftausgleich und Kraft im Allgemeinen gemacht. Die Gruppe, die mit ihrem Schätzungsergebnis, wie viel der Kran tragen kann, am nähesten liegt hat gewonnen.
Materialien
- kurze, dickere Strohalme ohne Knick
- Strohalme mit Knick
- Holzplatte
- Pappdeckel
- Tesafilm
- Heißklebepistole
Inspiration
Skizze Vorderseite
Konstruktion
Der Kran ist rechteckig, anstatt von quadratischer Form. Wir haben, für jeweils eine Seite des Bausteins des unteren Teils zwei kleine Konstruktionen erstellt: 1 Loch in die Mitte eines langen, dicken Strohhalmes gebohrt und einen anderen dicken Strohhalm dadurch gesteckt, sozusagen eine X-Form erstellt. Diese 2 Strohhalm-Konstruktionen "X" haben wir miteinander verbunden und dann oben
Wir haben uns überlegt, dass sich die Strohhalme kreuzen, damit sich die Kräfte gegeseitig aufheben. Dies geschieht, weil die Kräfte, einmal die nach unten drücken und die, die nach oben drücken ( in der Zeichnung mit Pfeilen dargestellt), gegeneinander wirken ( das kann man in der Skizze anhand der Pfeile die gegeneinander zeigen sehen ). Dadurch werden sie aufgehoben und die einzelnen Stockwerke des Krans brechen nicht zusammen. Das ist wie wenn man seine Hände zusammen drückt, dabei werden auch die Kräfte aufgehoben, sodass die Hände nicht zur einen Seite gedrückt werden, sondern in der Mitte bleiben. Die Kräfte werden allerdings nur aufgehoben, wenn beide wirkenden Kräfte die gleiche Stärke haben, wenn das nicht der Fall ist, wird die eine Seite, von der die schwächere Kraft aus wirkt, weggedrückt, weil die andere Kraft stärker ist.
Rechnung zur Tragekraft des später fertigen Krans
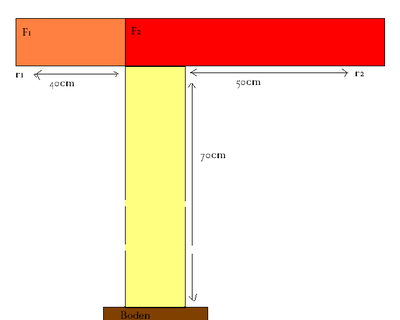
70cm lang ist der Fuß des Krans, 50cm der Tragarm.
F1 (Lastarm 1-Kraft): 10N F2(Lastarm 2-Kraft): ? r1(Länge der Lastarme): 50cm r2: 40 cm
-> Um das Ergebnis rauszubekommen, wie viel F2 tragen kann, haben wir die Länge und Kraft des Lastarms gefunden.
Formel: F1 * r1=F2*r2
Einsetzen der Längen: 10N*50cm=F2*40cm
F2 = 10*50/40 = 500/40
Ergebnis: F2=12,5N
Somit kann unser Kran eine Kraft von 12,5 Newton tragen!