Kräfte und die Statik eines Krans: Unterschied zwischen den Versionen
Vieth1 (Diskussion | Beiträge) (→Gewicht/Gegengewicht) |
(kat Mechanik) |
||
| (5 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 66: | Zeile 66: | ||
==Endergebnis== | ==Endergebnis== | ||
Wenn man jetzt also die 2,95kg Gegengewicht mit dem Hebegewicht 0,59kg addiert, kommt man auf ein Insgesamtgewicht von 3,54kg. Unser Kran kann theoretisch also 0,59kg heben. | Wenn man jetzt also die 2,95kg Gegengewicht mit dem Hebegewicht 0,59kg addiert, kommt man auf ein Insgesamtgewicht von 3,54kg. Unser Kran kann theoretisch also 0,59kg heben. | ||
| + | |||
| + | == Noch ein Kran == | ||
| + | Eine andere Gruppe hat sich durch dieses Bild inspirieren lassen und ist zu den unten stehnden Ergebnissen gekommen | ||
| + | |||
| + | [[Bild:Crane.jpg | 353px ]] | ||
| + | |||
| + | == '''Skizze Vorderseite'''== | ||
| + | |||
| + | |||
| + | <gallery> | ||
| + | Bild:DSCN2750.JPG|[[Skizze des 1. Stockwerks des Gerüstes]]</gallery> | ||
| + | |||
| + | [[Bild:Kran_1234567890.jpg | 400 px ]] | ||
| + | |||
| + | |||
| + | == '''Konstruktion''' == | ||
| + | |||
| + | |||
| + | Der Kran ist rechteckig, anstatt von quadratischer Form. Wir haben, für jeweils eine Seite des Bausteins des unteren Teils zwei kleine Konstruktionen erstellt: 1 Loch in die Mitte eines langen, dicken Strohhalmes gebohrt und einen anderen dicken Strohhalm dadurch gesteckt, sozusagen eine X-Form erstellt. Diese 2 Strohhalm-Konstruktionen "X" haben wir miteinander verbunden und dann oben | ||
| + | |||
| + | Wir haben uns überlegt, dass sich die Strohhalme kreuzen, damit sich die Kräfte gegeseitig aufheben. Dies geschieht, weil die Kräfte, einmal die nach unten drücken und die, die nach oben drücken ( in der Zeichnung mit Pfeilen dargestellt), gegeneinander wirken ( das kann man in der Skizze anhand der Pfeile die gegeneinander zeigen sehen ). Dadurch werden sie aufgehoben und die einzelnen Stockwerke des Krans brechen nicht zusammen. Das ist wie wenn man seine Hände zusammen drückt, dabei werden auch die Kräfte aufgehoben, sodass die Hände nicht zur einen Seite gedrückt werden, sondern in der Mitte bleiben. Die Kräfte werden allerdings nur aufgehoben, wenn beide wirkenden Kräfte die gleiche Stärke haben, wenn das nicht der Fall ist, wird die eine Seite, von der die schwächere Kraft aus wirkt, weggedrückt, weil die andere Kraft stärker ist. | ||
| + | |||
| + | |||
| + | == '''''Rechnung zur Tragekraft des später fertigen Krans''' == | ||
| + | |||
| + | '' | ||
| + | |||
| + | 70cm lang ist der Fuß des Krans, 50cm der Tragarm. | ||
| + | |||
| + | '''F1 (Lastarm 1-Kraft):''' 10N | ||
| + | '''F2(Lastarm 2-Kraft):''' ? | ||
| + | '''r<sub>1</sub>(Länge der Lastarme):''' 50cm | ||
| + | '''r<sub>2</sub>:''' 40 cm | ||
| + | |||
| + | -> Um das Ergebnis rauszubekommen, wie viel F2 tragen kann, haben wir die Länge und Kraft des Lastarms gefunden. | ||
| + | |||
| + | ''Formel'': F1 * r<sub>1</sub>=F2*r<sub>2</sub> | ||
| + | |||
| + | ''Einsetzen der Längen:'' 10N*50cm=F2*40cm | ||
| + | |||
| + | '''F2''' = 10*50/40 = 500/40 | ||
| + | |||
| + | ''Ergebnis:'' '''F2=12,5N''' | ||
| + | |||
| + | Somit kann unser Kran eine Kraft von '''12,5''' Newton tragen! | ||
| + | |||
| + | [[Kategorie:Mechanik]] | ||
| + | [[Kategorie:Statik]] | ||
Aktuelle Version vom 7. Januar 2013, 21:02 Uhr
Inhaltsverzeichnis |
Aufgabe
Zu unser Unterrichtsreihe zu Thema Kraft [1] bzw. Kraftverteilung sollten wir einen Kran bauen und auch möglichst genau sagen können wie viel er heben kann. Welche Gruppe am Ende die Belastbarkeit ihres Krans am besten geschätzt hat, hat gewonnen. Es ging nicht darum welcher Kran am meisten Heben konnte.
Der Kran
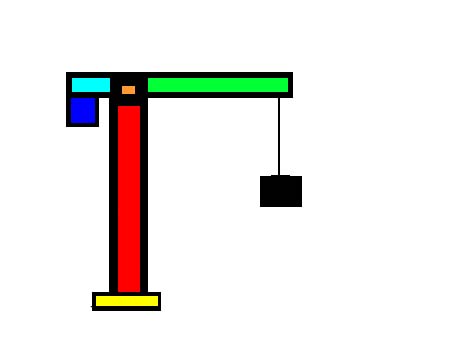
Die Konstruktion durfte nur aus Plastikstrohhalmen und Kleber unserer Wahl bestehen, außerdem sollte der Kran mit einer Seilwinde Gewichte hochziehen können. Der Stamm (rot) sollte eine Länge von 70cm haben und der Arm (hellblau/grün) eine Länge von insgesamt 60cm: 10cm Kraftarm (hellblau) und 50cm Lastarm (grün). Die Stelle, ander sich der orange Punkt befindet, ist normalerweise beweglich, dies musste bei uns aber nicht der Fall sein. Das Gegengewicht (blau) befindet sich am Kraftarm. Die Basis (gelb) wird auf einer Holzplatte befestigt und diese an einem Tisch, damit der Krahn nicht umfällt und wir an die Basis nicht weitere Gewichte machen müssen.
Unser Kran
Durchführung
Stamm
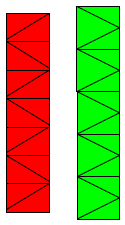
Unser erster Schritt beim Bauen des Krans war das ansehen von verschiedenen Krantypen, letztendlich haben wir uns für einen Kran entschieden, der den Stamm in mehrere Stockwerke eingeteilt hatte (rot). Da uns die Umsetzung mit so vielen Querstreben zu mühselig war, haben wir es ein wenig umgeändert (grün) und jede zweite Strebe herausgelassen. Im nächsten Schritt haben wir die Maße festgelegt. Wir haben uns für einen Würfel mit den Maßen: 10cmx10cmx10cm entschieden, da wir der Stamm 70cm hoch werden muss, fanden wir die Größe passend, denn sind die Strohhalme zu kurz hat es in die Höhe keine Stabilität und wenn die Strohhalme zu lang sind, ist Gefahr, das die Strohhalme schnell knicken, groß. Die Enden haben wir mit der Heißklebepistole fixiert. Wir haben den fertigen Würfel von oben Belastet und er konnte 3,7kg halten und brach dann zusammen.
Erst war er auf 1/3 seines ursprünglichen Volumens zusammengestaucht und hat sich dann wieder entfaltet.
Arm
Den Arm wollten wir aus den gleichen Dreiecken machen wie beim Würfel. Allerdings sollte dieser nicht quadratisch sondern dreieckig werden. Das bedeutet, dass wir nicht vier sondern drei Dreiecke aneinader kleben wollten. Die Dreiecke sollten mit der Spitze nach oben zeigen.
Auswertung
Allgemein
Wir haben uns entschieden, unseren Kran aus Dreiecken zu konstruieren, da diesen die Kaft am besten verteilen.
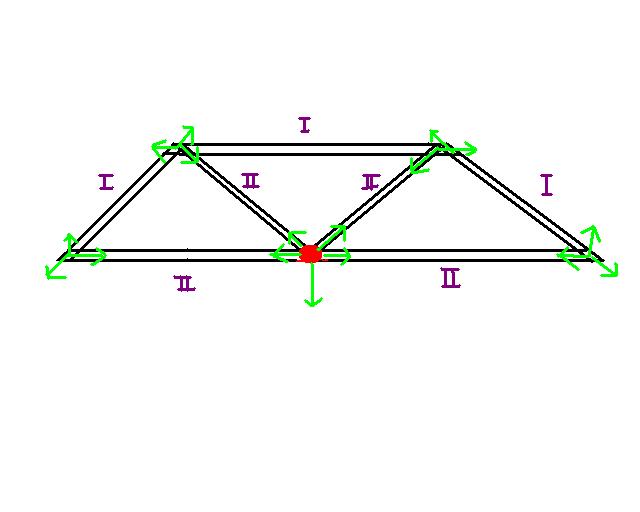
Druck- und Zugstab
Bei der Kraftverteilung im Kran gibt es in den Dreiecken zwei verschiedene Arten von Stäben: die Druck- und die Zugstäbe. Diese sind ganz einfach zu definieren: der Druckstab drückt die anderen Stäbe auseinander und der Zugstab zieht sie zusammen. Die mit einer 1 gekennzeichneten Stäbe sind Druckstäbe und die mit einer 2 sind Zugstäbe. Die Krafteinwirkung befindet sich in der Zeichnung am roten Punkt. Die Pfeile zeigen wie sich die Kraft verteilt. Um zu entscheiden welcher der Druck- und welcher Zugstab ist muss man sich die Kraftverteilung ansehen. Die Stellen, an denen die Stäbe verbunden sind, nennt man Knoten.
Ergebnis
Gewicht/Gegengewicht
Da wir unsere Experimente nicht zu Ende führen konnten, führen wir nur eine Beispielrechnung zum Gegengewicht durch, in der wir annehmen, dass unser Arm genauso viel tragen kann wie unser Stamm, 3,7kg bzw. haben wir 0,2kg abgezogen wegen eventuellen Ausführungsfehlern. Dazu haben wir uns eine Formel überlegt:
(a*b)/c=g
a =Das Gewicht, dass der Kran tragen kann
b =Die Länge der Lastseite
c =Der Abstand auf der Kraftseite
g =Gegengewicht
Um das Gegengewicht g zu ermitteln, haben wir für a verschiedene Zahlen so eingesetzt,dass das ermittelte Gegengewicht zusammen mit unserem Wert a möglichst nah an den 3,5kg ist. Unsere Endrechnung:
(0,59*50)/10= 2,95kg
Also beträgt unser Gegengewicht 2,95kg.
Eine weitere Berechnung einer anderen Gruppe hat folgendes ergeben:
Berechnung der Belastbarkeit:
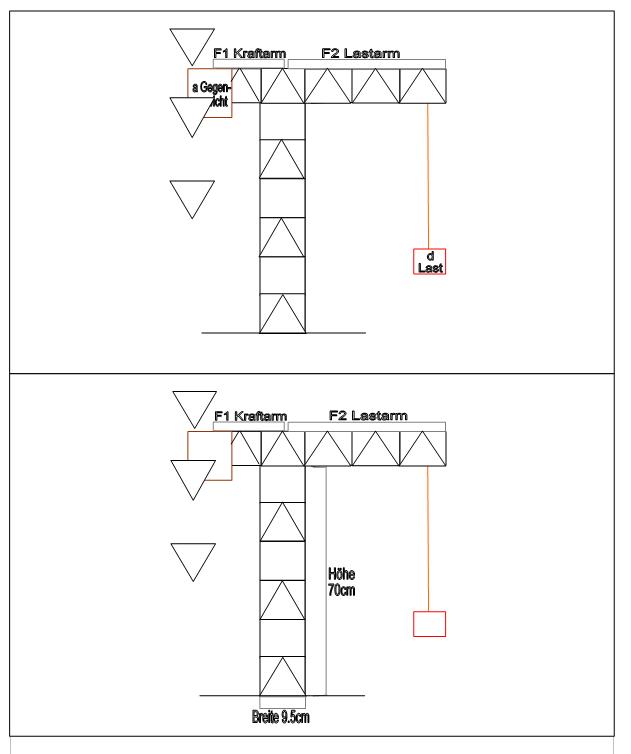
Kranarm:
c = Länge des Lastarms (F2) = 50cm
b = Länge des Kraftarms (F1) = 15cm
a = Gegengewicht
d = Last
Formel: 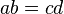
a 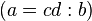 |
d 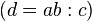
|
|---|---|
| 10/3 kg | 1 kg |
| 5 kg | 1.5 kg |
Endergebnis
Wenn man jetzt also die 2,95kg Gegengewicht mit dem Hebegewicht 0,59kg addiert, kommt man auf ein Insgesamtgewicht von 3,54kg. Unser Kran kann theoretisch also 0,59kg heben.
Noch ein Kran
Eine andere Gruppe hat sich durch dieses Bild inspirieren lassen und ist zu den unten stehnden Ergebnissen gekommen
Skizze Vorderseite
Konstruktion
Der Kran ist rechteckig, anstatt von quadratischer Form. Wir haben, für jeweils eine Seite des Bausteins des unteren Teils zwei kleine Konstruktionen erstellt: 1 Loch in die Mitte eines langen, dicken Strohhalmes gebohrt und einen anderen dicken Strohhalm dadurch gesteckt, sozusagen eine X-Form erstellt. Diese 2 Strohhalm-Konstruktionen "X" haben wir miteinander verbunden und dann oben
Wir haben uns überlegt, dass sich die Strohhalme kreuzen, damit sich die Kräfte gegeseitig aufheben. Dies geschieht, weil die Kräfte, einmal die nach unten drücken und die, die nach oben drücken ( in der Zeichnung mit Pfeilen dargestellt), gegeneinander wirken ( das kann man in der Skizze anhand der Pfeile die gegeneinander zeigen sehen ). Dadurch werden sie aufgehoben und die einzelnen Stockwerke des Krans brechen nicht zusammen. Das ist wie wenn man seine Hände zusammen drückt, dabei werden auch die Kräfte aufgehoben, sodass die Hände nicht zur einen Seite gedrückt werden, sondern in der Mitte bleiben. Die Kräfte werden allerdings nur aufgehoben, wenn beide wirkenden Kräfte die gleiche Stärke haben, wenn das nicht der Fall ist, wird die eine Seite, von der die schwächere Kraft aus wirkt, weggedrückt, weil die andere Kraft stärker ist.
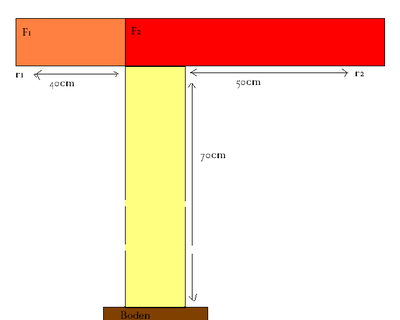
Rechnung zur Tragekraft des später fertigen Krans
70cm lang ist der Fuß des Krans, 50cm der Tragarm.
F1 (Lastarm 1-Kraft): 10N F2(Lastarm 2-Kraft): ? r1(Länge der Lastarme): 50cm r2: 40 cm
-> Um das Ergebnis rauszubekommen, wie viel F2 tragen kann, haben wir die Länge und Kraft des Lastarms gefunden.
Formel: F1 * r1=F2*r2
Einsetzen der Längen: 10N*50cm=F2*40cm
F2 = 10*50/40 = 500/40
Ergebnis: F2=12,5N
Somit kann unser Kran eine Kraft von 12,5 Newton tragen!