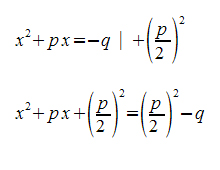G14: Lösen quadratischer Gleichungen: Unterschied zwischen den Versionen
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) | |||
| Zeile 18: | Zeile 18: | ||
Wenn man die qudratische Gleichung mit der p-q-Formel lösen möchte, sollte man den folgnden Weg benutzen um die unbekannten Variablen zu errechnen: | Wenn man die qudratische Gleichung mit der p-q-Formel lösen möchte, sollte man den folgnden Weg benutzen um die unbekannten Variablen zu errechnen: | ||
| − | |||
| − | |||
| + | Ein Video zur besseren Erläuterung: | ||
| − | + | {{#ev:youtube|4grbGixuSXM}} | |
| + | Quelle: [http://www.youtube.com/watch?v=4grbGixuSXM YouTube] | ||
| + | |||
| + | Anschließend sollte man noch die Probe machen, um sicher zu gehen, dass man keinen Rechenfehler gemacht hat. | ||
===LÖsen mit der qudratischen Ergänzung=== | ===LÖsen mit der qudratischen Ergänzung=== | ||
Aktuelle Version vom 13. Februar 2012, 14:42 Uhr
Inhaltsverzeichnis |
Definition quadratischer Gleichungen
Wenn in einer ganzrationalen Gleichung, ohne x im Nenner von Brüchen, die Unbekannte mit der Hochzahl 2 auftritt, also z.B. als x², und dieses x² auch nicht durch Umformungen wegfällt, spricht man von einer quadratischen Gleichung. Bei dieser kommt die Variable x mindestens einmal in der 2.Potenz vor, aber nicht höher. Die Normalform der qudratischen Gleichung ist immer: ax² + px + q = 0
Natürlich darf die Variable a nicht gleich Null sein, denn dann würde der erste Summand wegfallen, und es würde eine lineare Gleichung vorliegen:
0·x2+8x+9=0 = 8x+9=0
Lösungsvarianten
Es giebt zwei verschiedene Varianten die quadratische Gleichung zu Lösen.
Lösen mit der p-q-Formel
Wenn man die qudratische Gleichung mit der p-q-Formel lösen möchte, sollte man den folgnden Weg benutzen um die unbekannten Variablen zu errechnen:
Ein Video zur besseren Erläuterung:
Quelle: YouTube
Anschließend sollte man noch die Probe machen, um sicher zu gehen, dass man keinen Rechenfehler gemacht hat.
LÖsen mit der qudratischen Ergänzung
Wenn man die qudratische Gleichung jedoch mit der qudratischen Ergänzung lösen möchte, sollte man den folgenden Weg benutzen: