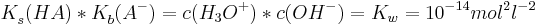Formelsammlung: Unterschied zwischen den Versionen

Aus KAS-Wiki
Wechseln zu: Navigation, Suche
(→‎Säurekonstanten und Basekonstanten)
(→‎Säurekonstanten und Basekonstanten)
 
(4 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt)
Zeile 31: Zeile 31:
 
und ebenso gilt analog für die Basekonstante <br /><br />
 
und ebenso gilt analog für die Basekonstante <br /><br />
 
<math>K_{b}^{ }=c(H_{2}O)*K=\frac {c(OH^{-})*c(BH^{+})}{c(B)}</math><br /><br />
 
<math>K_{b}^{ }=c(H_{2}O)*K=\frac {c(OH^{-})*c(BH^{+})}{c(B)}</math><br /><br />
−
wobei alle Konzentrationen auf das Gleichgewicht bezogen sind.<br />
+
wobei alle Konzentrationen auf das Gleichgewicht bezogen sind.<br /><br />
 
Man definiert weiter den <math>pK_{s}^{ }</math>-Wert als <br /><br />
 
Man definiert weiter den <math>pK_{s}^{ }</math>-Wert als <br /><br />
−
<math>pK_{s}^{ }=-\lg K_{s}</math>
+
<math>pK_{s}^{ }=-\lg K_{s}</math><br /><br />
 +
und den <math>pK_{b}^{ }</math>-Wert als <br /><br />
 +
<math>pK_{b}^{ }=-\lg K_{b}</math><br /><br />
 +
und erhält auch hier die Beziehung <br /><br />
 +
<math>pK_{s}^{ }(HA)+pK_{b}(A^{-})=14</math><br /><br />
 +
und<br /><br />
 +
<math>K^{ }_{s}(HA)*K^{ }_{b}(A^{-})=c(H_{3}O^{+})*c(OH^{-})=K_{w}=10^{-14}mol^{2}l^{-2}</math><br /><br />

Aktuelle Version vom 11. April 2010, 12:52 Uhr

Inhaltsverzeichnis

Potentiometrie

Sei 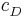c_{D}^{ } die Konzentration in der Donator-Halbzelle, dessen Konzentration bestimmt werden soll. Dann gilt

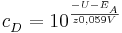
c_{D}^{ }=10^{\frac{-U-E_{A}^{ }}{z 0,059V}}

wobei 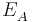E_{A}^{ } das vorher bestimme Elektrodenpotential der Akzeptorhalbzelle ist und 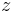z_{ }^{ } die Elektronenübertragungszahl.

Herleitung

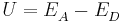
U=E_{A}^{ }-E_{D}^{ }
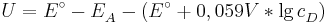
U=E^{\circ}-E_{A}^{ }-(E^{\circ}+0,059V*\lg c_{D}^{ })
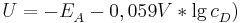
U=-E_{A}^{ }-0,059V*\lg c_{D}^{ })
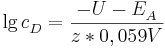
\lg c_{D}^{ }=\frac {-U-E_{A}^{ }}{z*0,059V}
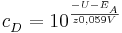
c_{D}^{ }=10^{\frac{-U-E_{A}^{ }}{z 0,059V}}

pH-Wert, pOH-Wert und Beziehungen

Für die Definition des pH-Wertes gilt

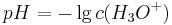
pH^{ }_{ }=-\lg{c(H_{3}O^{+})}

und es gilt analog

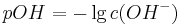
pOH^{ }_{ }=-\lg{c(OH_{ }^{-})}

wobei sich folgende Beziehung ergibt

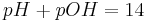
pH_{ }^{ }+pOH=14

Dies folgt nämlich aus der Tatsache, dass für das Ionenprodukt des Wassers gilt

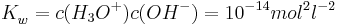
K^{ }_{w}=c(H_{3}O^{+})c(OH_{ }^{-})=10^{-14}mol^{2}l^{-2}

und dem Anwenden der Logarithmus-Gesetze.

Säurekonstanten und Basekonstanten

Die Säurekonstante 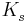K_{s}^{ } ist definiert als

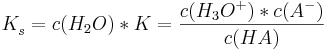
K_{s}^{ }=c(H_{2}O)*K=\frac {c(H_{3}O^{+})*c(A^{-})}{c(HA)}

und ebenso gilt analog für die Basekonstante

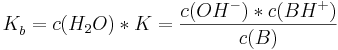
K_{b}^{ }=c(H_{2}O)*K=\frac {c(OH^{-})*c(BH^{+})}{c(B)}

wobei alle Konzentrationen auf das Gleichgewicht bezogen sind.

Man definiert weiter den 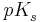pK_{s}^{ }-Wert als

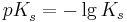
pK_{s}^{ }=-\lg K_{s}

und den 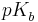pK_{b}^{ }-Wert als

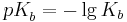
pK_{b}^{ }=-\lg K_{b}

und erhält auch hier die Beziehung

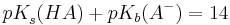
pK_{s}^{ }(HA)+pK_{b}(A^{-})=14

und

K^{ }_{s}(HA)*K^{ }_{b}(A^{-})=c(H_{3}O^{+})*c(OH^{-})=K_{w}=10^{-14}mol^{2}l^{-2}

Von „http://kas.zum.de/index.php?title=Formelsammlung&oldid=2776“