GK11 2014/15: Unterschied zwischen den Versionen
Rbugaj (Diskussion | Beiträge) (→Lorentzkraft auf stromdurchflossene Leiter) |
Rbugaj (Diskussion | Beiträge) (→Massenspektrographie) |
||
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
auf dieser Seite werden nochmal die Arbeitsblätter, Aufgaben (mit Lösungen) und Dokumente hochgeladen, mit denen wir während meines Unterrichts im Dezember und Januar gearbeitet haben... | auf dieser Seite werden nochmal die Arbeitsblätter, Aufgaben (mit Lösungen) und Dokumente hochgeladen, mit denen wir während meines Unterrichts im Dezember und Januar gearbeitet haben... | ||
Grüße, Robert Bugaj | Grüße, Robert Bugaj | ||
| + | |||
| + | Nachtrag: Die Lösungen lade ich immer hoch, wenn ich etwas Zeit habe... Zur Klausur sollte aber alles rechtzeitig vorhanden sein! | ||
=Bewegte Ladung im Magnetfeld= | =Bewegte Ladung im Magnetfeld= | ||
| Zeile 63: | Zeile 65: | ||
Rechenaufgaben zur Massenspektrographie finden sich hier: | Rechenaufgaben zur Massenspektrographie finden sich hier: | ||
| + | http://wikis.zum.de/kas/Datei:Rechenaufgaben_Massenspektrograph.pdf | ||
Die Lösungen zu den Aufgaben finden sich hier: | Die Lösungen zu den Aufgaben finden sich hier: | ||
| + | http://wikis.zum.de/kas/Datei:L%C3%B6sungen_der_Rechenaufgaben_zur_Massenspektrographie.pdf | ||
Aktuelle Version vom 5. Februar 2015, 15:19 Uhr
Lieber Physik GK11 von Herrn Vieth, auf dieser Seite werden nochmal die Arbeitsblätter, Aufgaben (mit Lösungen) und Dokumente hochgeladen, mit denen wir während meines Unterrichts im Dezember und Januar gearbeitet haben... Grüße, Robert Bugaj
Nachtrag: Die Lösungen lade ich immer hoch, wenn ich etwas Zeit habe... Zur Klausur sollte aber alles rechtzeitig vorhanden sein!
Inhaltsverzeichnis |
Bewegte Ladung im Magnetfeld
Lorentzkraft auf stromdurchflossene Leiter
In einem Demonstrationsversuch mit einem stromdurchflossenen Leiter zwischen den Polen eines Hufeisenmagnets wurde festgestellt, dass das Magnetfeld eine Kraft auf den Leiter ausübt.
Mit Hilfe einer weiteren Versuchsreihe sollte die Formel für die Lorentzkraft auf stromdurchflossene Leiter ermittelt werden. Ergebnis:
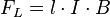 .
.
Dabei bezeichnet l die Leiterlänge im Metern, I die Leiterstromstärke in Ampère und B die magnetische Flussdichte.
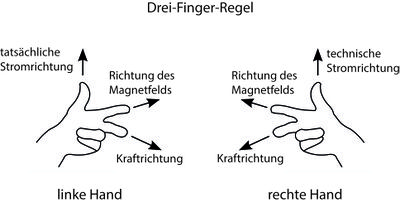
Die Richtung der Lorentzkraft kann mit der Drei-Finger-Regel ermittelt werden.
Aufgaben zur Lorentzkraft auf stromdurchflossene Leiter finden sich hier: http://wikis.zum.de/kas/Datei:Aufgabenblatt_zur_Lorentzkraft_auf_stromdurchflossene_Leiter.pdf
Eine weitere Aufgabe findet sich hier: http://wikis.zum.de/kas/Datei:Aufgabe_zur_Wiederholung_der_Lorentzkraft_auf_stromdurchflossene_Leiter.pdf
Die Lösungen zu den Aufgaben finden sich hier: http://wikis.zum.de/kas/Datei:L%C3%B6sung_zu_Aufgabe_2_Lorentzkraft.pdf
Lorentzkraft auf freie Ladungsträger
Herleitung der Formel
Die Lorentzkraft wird jetzt auch für freie Ladungsträger, zunächst Elektronen, betrachtet. Die Formel für den Betrag der Lorentzkraft lautet dann
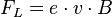 .
.
Hierbei ist e die Ladung des Elektrons (Elementarladung) und v seine Geschwindigkeit. B bezeichnet wieder die magnetische Flussdichte. Die Anleitung für die Herleitung findet sich hier: http://wikis.zum.de/kas/Datei:Anleitung_Herleitung_Formel_Lorentzkraft_auf_freie_Ladungstr%C3%A4ger.pdf
Die Richtung der Lorentzkraft kann wieder mit der Drei-Finger-Regel ermittelt werden.
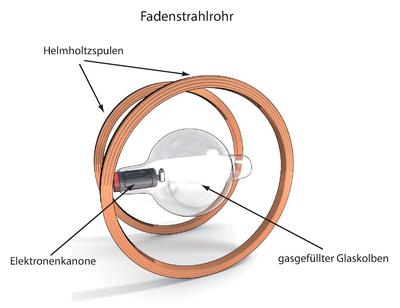
Fadenstrahlrohr
Ein Fadenstrahlrohr lässt sich schematisch wie folgt darstellen:
Das Arbeitsblatt mit den Hypothesen über die Bahn der Elektronen im Fadenstrahlrohr findet sich hier: http://wikis.zum.de/kas/Datei:Arbeitsblatt_Hypothesen_Fadenstrahlrohr.pdf
Dass sich im Fadenstrahlrohr (bei entsprechender Geschwindigkeit bzw. ausreichender magnetischer Flussdichte) eine Kreisbahn ergibt, wurde anhand des nächsten Arbeitsblatts erarbeitet: http://wikis.zum.de/kas/Datei:Arbeitsblatt_Erkl%C3%A4rung_Fadenstrahlrohr.pdf
Bestimmung der Elektronenmasse
Mit Hilfe des Fadenstrahlrohrs konnte über die Messung der Radien der Kreisbahnen der Elektronen ihre Masse bestimmt werden. Die Anleitung für die Herleitung der notwendigen Formel zur Berechnung findet sich hier: http://wikis.zum.de/kas/Datei:Arbeitsblatt_Herleitung_Formel_Massenbestimmung_Elektron.pdf
Der Literaturwert für die Masse eines Elektrons liegt bei
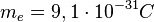 ,
,
unser mit vergleichsweise einfachen Mitteln ermittelter Wert lag bei
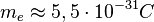 .
.
Da wir immerhin in der richtigen Größenordnung liegen, können wir mit unserem Ergebnis zufrieden sein.
Massenspektrographie
Ähnlich wie bei der Massenbestimmung des Elektrons im Fadenstrahlrohr kann mit einem Massenspektrographen die Masse von anderen geladenen Teilchen bestimmt werden (bspw. Ionen von Gasatomen oder alpha-Teilchen). Wir formulieren die Formel für die Lorentzkraft auf ein freies geladenes Teilchen nun
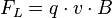 ,
,
q gibt uns dann die Ladung des Teilchens an.
Im folgenden Arbeitsblatt ist der Aufbau eines (Bainbridge-)Massenspektrographen schematisch dargestellt: http://wikis.zum.de/kas/Datei:Arbeitsblatt_Massenspektrograph.pdf
Auf der folgenden Seite finden sich Simulationen mit Erläuterungen zum Geschwindigkeitsfilter und zum Massenspektrographen, die die Fragen auf dem Arbeitsblatt beantworten und helfen, die Funktionsweise eines Massenspektrographen zu verstehen:
Rechenaufgaben zur Massenspektrographie finden sich hier: http://wikis.zum.de/kas/Datei:Rechenaufgaben_Massenspektrograph.pdf
Die Lösungen zu den Aufgaben finden sich hier: http://wikis.zum.de/kas/Datei:L%C3%B6sungen_der_Rechenaufgaben_zur_Massenspektrographie.pdf