Affine Abbildungen: Unterschied zwischen den Versionen
Aus KAS-Wiki
(farbige Überschrift) |
|||
| (3 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 21: | Zeile 21: | ||
<math>\vec x_2\,'=a_2x_1+b_2x_2+c_2</math> | <math>\vec x_2\,'=a_2x_1+b_2x_2+c_2</math> | ||
| + | |||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | ! Abbildung || Flächeninhalt || Fixpunkte, Fixgeraden || Matrixdarstellung | ||
| + | |- | ||
| + | | Spiegelung an der Ursprungsgeraden || A bleibt gleich || (0/0) Spiegelgerade (Fixgerade) || <math>M=\begin{pmatrix} cos2\varphi & sin2\varphi \\ sin2\varphi & -cos2\varphi \end{pmatrix}</math> | ||
| + | |- | ||
| + | | zentrische Streckung || <math>\!A'= 3^2A</math> || (0/0) x-und y-Achse jede Gerade <math>y=a*x</math> || <math>M*\begin{pmatrix} k & 0 \\ 0 & k \end{pmatrix}</math> | ||
| + | |- | ||
| + | | Drehung || A bleibt gleich || (0/0) || <math>M=\begin{pmatrix} cos\varphi & sin\varphi \\ -sin\varphi & cos\varphi \end{pmatrix}</math> | ||
| + | |- | ||
| + | | Skalierung || <math>\!A'=2*4A</math> || (0/0) x- und y-Achse | ||
| + | |- | ||
| + | | Scherung || <math>\!A'=A</math> || (0/0) x- oder y-Achse | ||
| + | |} | ||
| + | <math>\varphi</math> ist der Winkel, um den die Funktion gespiegelt bzw. gedreht wird. | ||
Aktuelle Version vom 7. Dezember 2009, 16:57 Uhr
Definition:
Eine geradentreue und umkehrbare geometrische Abbildung der Ebene auf sich selbst nennt man eine affine Abbildung oder Affinität.
Die affine Abbildung bildet ein neues Koordinatensystem.
Die einzelnen Spalten der Matrix dürfen nicht linear abhängig sein.
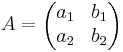
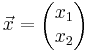

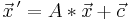
LGS:
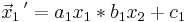
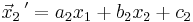
| Abbildung | Flächeninhalt | Fixpunkte, Fixgeraden | Matrixdarstellung |
|---|---|---|---|
| Spiegelung an der Ursprungsgeraden | A bleibt gleich | (0/0) Spiegelgerade (Fixgerade) | 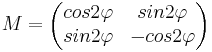
|
| zentrische Streckung | 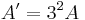 |
(0/0) x-und y-Achse jede Gerade 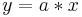 |
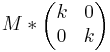
|
| Drehung | A bleibt gleich | (0/0) | 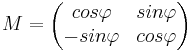
|
| Skalierung | 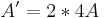 |
(0/0) x- und y-Achse | |
| Scherung | 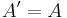 |
(0/0) x- oder y-Achse |
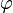 ist der Winkel, um den die Funktion gespiegelt bzw. gedreht wird.
ist der Winkel, um den die Funktion gespiegelt bzw. gedreht wird.

