Kurvendiskussion von Funktionsscharen: Unterschied zwischen den Versionen

Aus KAS-Wiki
Wechseln zu: Navigation, Suche
 
(6 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt)
Zeile 9: Zeile 9:
 
               <math>\frac{-t}{3}=\frac{-1}{18}x_2 </math>
 
               <math>\frac{-t}{3}=\frac{-1}{18}x_2 </math>
 
               <math>6t=x_2</math>
 
               <math>6t=x_2</math>
 +
 +
 +
 +
Extremstellen: <math>f_t'(x)=0</math>
 +
             
 +
              <math>0=\frac{-2}{9}x^3+tx^2</math>
 +
              <math>0=x^2(\frac{-2}{9}x+t)</math> 
 +
              <math>0=\frac{-2}{9}x+t</math>  v    <math>0=x^2</math>  =>  x<sub>1</sub>=0
 +
              <math>x_2=\frac{9}{2}t</math>
 +
 +
Zu prüfen ist:
 +
              <math>f_t''(x_1)=0</math>                =>  Sattelpunkt
 +
              <math>f_t''(x_2)=\frac{-9}{2}t^2</math>  =>  für <math>t\ne0</math>        Hochpunkt
 +
                                      für <math>t=0</math>          Sattelpunkt
 +
 +
 +
 +
Wendepunkte: <math>f_t''(x)=0</math>

Aktuelle Version vom 23. November 2010, 14:00 Uhr

Kurvendiskussion an der Funktionsschar: 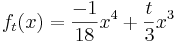f_t(x)=\frac{-1}{18}x^4+\frac{t}{3}x^3

Nullstellen: 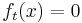f_t(x)=0 

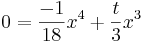
             0=\frac{-1}{18}x^4+\frac{t}{3}x^3
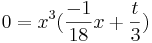
             0=x^3(\frac{-1}{18}x+\frac{t}{3}) 
             \frac{-1}{18}x+\frac{t}{3}=0    v    x^3=0 => x1=0
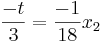
             \frac{-t}{3}=\frac{-1}{18}x_2 
             6t=x_2


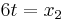
Extremstellen: 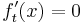f_t'(x)=0 

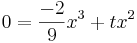
              0=\frac{-2}{9}x^3+tx^2
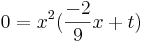
              0=x^2(\frac{-2}{9}x+t)  
              0=\frac{-2}{9}x+t   v    0=x^2   =>  x1=0
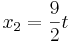
              x_2=\frac{9}{2}t

Zu prüfen ist: 

              f_t''(x_1)=0                 =>   Sattelpunkt
              f_t''(x_2)=\frac{-9}{2}t^2   =>   für t\ne0        Hochpunkt 
                                      für t=0          Sattelpunkt


Wendepunkte: f_t''(x)=0

Von „http://kas.zum.de/index.php?title=Kurvendiskussion_von_Funktionsscharen&oldid=4867“