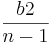Ziehen mit Reihenfolge ohne Zurücklegen.: Unterschied zwischen den Versionen

Aus KAS-Wiki
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: == Beispiel: Ziehen ohne Zurückleggen == <u>mit Reihenfolge</u> '''<u>Beispiel:</u>''' In einer Urne befinden sich sechs blaue Kugeln und vier gelbe. Nun soll man mit...)
 
(Kategorie:Stochastik; typo)
 
Zeile 1: Zeile 1:
−
== Beispiel: Ziehen ohne Zurückleggen ==
+
== Beispiel: Ziehen ohne Zurücklegen ==
  
 
<u>mit Reihenfolge</u>
 
<u>mit Reihenfolge</u>
Zeile 27: Zeile 27:
 
p1=<math>\frac{a1}{n}</math>;
 
p1=<math>\frac{a1}{n}</math>;
 
q2=<math>\frac{b2}{n-1}</math>
 
q2=<math>\frac{b2}{n-1}</math>
 +
 +
 +
 +
[[Kategorie:Stochastik]]

Aktuelle Version vom 27. Dezember 2010, 10:57 Uhr

Beispiel: Ziehen ohne Zurücklegen

mit Reihenfolge Beispiel: In einer Urne befinden sich sechs blaue Kugeln und vier gelbe. Nun soll man mit geschlossenen Augen fünf Kugeln ziehen ohne diese dabei zurückzulegen. Frage: 1.Wie groß ist die Wahrscheinlichkeit 

      a.)hintereinander drei gelbe und zwei blaue Kugel zu ziehen?

Rechnung zu a) Wahrscheinlichkeit eine gelbe Kugel zu ziehen: 

              p(g)=\frac{4}{10} 

              Wahrscheinlichkeit eine blaue Kugel zu ziehen:
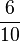
              p(b)=\frac{6}{10}

Nun muss man die Wahrscheinlichkeiten miteinander multiplizieren. Wahrscheinlichkeit für: 

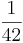
p(g,g,g,b,b)=\frac{4}{10}*\frac{3}{9}*\frac{2}{8}*\frac{6}{7}*\frac{5}{6}= \frac{1}{42}

Antwort:Die Wahrscheinlichkeit drei gelbe und zwei blaue zu ziehen beträgt ca. 2,38%.


Allgemeine Formel:

P({a1;b2;...})=p1*q2*...

p1=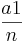\frac{a1}{n}; q2=\frac{b2}{n-1}

Von „http://kas.zum.de/index.php?title=Ziehen_mit_Reihenfolge_ohne_Zurücklegen.&oldid=5051“