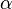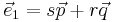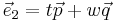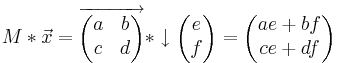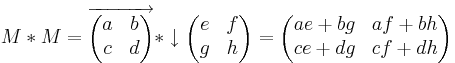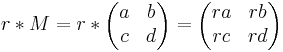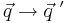Affine Abbildungen und deren Eigenschaften.: Unterschied zwischen den Versionen
Georg1 (Diskussion | Beiträge) |
(Kategorie:Lineare Algebra) |
||
| (13 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
'''''Affine Abbildungen''''' | '''''Affine Abbildungen''''' | ||
| − | + | ||
| + | == Definition == | ||
| + | |||
Affine Abbildungen sind geometrische Projektionen. Mit Hilfe von ''Abbildungsmatrizen'' wird ein geometrischer Prozess wie z.B. Spiegelungen, Drehungen um beliebige Zentren, Streckungen oder Stauchungen mathematisch erfasst und beschrieben. Um mit ihnen umgehen zu können bedarf es der ''Rechenregeln für Matrizen''. | Affine Abbildungen sind geometrische Projektionen. Mit Hilfe von ''Abbildungsmatrizen'' wird ein geometrischer Prozess wie z.B. Spiegelungen, Drehungen um beliebige Zentren, Streckungen oder Stauchungen mathematisch erfasst und beschrieben. Um mit ihnen umgehen zu können bedarf es der ''Rechenregeln für Matrizen''. | ||
| − | + | ||
| + | |||
| + | == Matrizenrechnung == | ||
| + | |||
| + | |||
Affine Abbildungen werden im zweidimensionelem Raum durch 2X2 Matrizen ausgedrückt. Sie haben die Form <math>\begin{pmatrix} | Affine Abbildungen werden im zweidimensionelem Raum durch 2X2 Matrizen ausgedrückt. Sie haben die Form <math>\begin{pmatrix} | ||
| − | a & c \\ | + | a & b \\ |
| − | b & d | + | c & d |
| − | \end{pmatrix}</math>. | + | \end{pmatrix}</math>. Für die affinen Abbildungen wichtige Rechenoperationen sind vor allem die Multiplikationen. Dabei gelten folgende Regeln: |
| + | |||
| + | <math>M*\vec x=\overrightarrow\begin{pmatrix} a & b \\ c & d \end{pmatrix}*\downarrow\begin{pmatrix} e \\ f \end{pmatrix}=\begin{pmatrix} ae+bf \\ ce+df \end{pmatrix}</math> | ||
| + | |||
| + | <math>M*M=\overrightarrow\begin{pmatrix} a & b \\ c & d \end{pmatrix}*\downarrow\begin{pmatrix} e & f \\ g & h \end{pmatrix}=\begin{pmatrix} ae+bg & af+bh \\ ce+dg & cf+dh \end{pmatrix}</math> | ||
| + | |||
| + | <math>r*M=r*\begin{pmatrix} a & b \\ c & d \end{pmatrix}=\begin{pmatrix} ra & rb \\ rc & rd \end{pmatrix}</math> | ||
| + | |||
| + | |||
| + | == Aufstellung einer Abbildungsmatrix == | ||
| + | |||
| + | Eine Abbildungsvorschrift wird durch eine Matrix in Multiplikation mit dem Ortsvektor zu einem beliebigen Punkt, sowie einer Addition eines eventuell vorkommenden Verschiebungsvektor, vollständig beschrieben: | ||
| + | <math>\vec x\,'=A*\vec x+\vec c</math>. | ||
| + | Häufig finden sich Rechenaufgaben, in denen Ihnen drei beliebige Punkte und deren Bildpunkte gegeben sind. Anhand dieser Bedingungen (drei punkte und ihre Bilder) lassen sich sämtliche Abbildungen mathematisch erfassen und wird es desweiteren möglich, eine Abbildungsvorschrift zu entwickeln. | ||
| + | Besonders einfach ist es dabei, die gegebenen Punkte und Bildpunkte durch eine Linearkombination der Einheitsvektoren darzustellen. Es gilt: die Bilder der Einheitsvektoren entsprechen den Spaltenvektoren der Abbildungsmatrix. | ||
| + | |||
| + | allgemeines Rechenbeispiel: gegeben sind <math>\vec p\rightarrow\vec p\ '</math><br /><math>0\rightarrow 0</math> | ||
| + | ::::::::::<math>\vec q\rightarrow\vec q\ '</math> | ||
| + | :::gesucht ist die Abbildungsmatrix <math>\alpha</math> | ||
| + | |||
| + | <br /><math>\vec e_1= s\vec p+r\vec q</math><br /><math>\vec e_2= t\vec p+w\vec q</math> | ||
| + | |||
| + | |||
| + | |||
| + | [[Kategorie:Lineare Algebra]] | ||
Aktuelle Version vom 27. Dezember 2010, 10:54 Uhr
Affine Abbildungen
Definition
Affine Abbildungen sind geometrische Projektionen. Mit Hilfe von Abbildungsmatrizen wird ein geometrischer Prozess wie z.B. Spiegelungen, Drehungen um beliebige Zentren, Streckungen oder Stauchungen mathematisch erfasst und beschrieben. Um mit ihnen umgehen zu können bedarf es der Rechenregeln für Matrizen.
Matrizenrechnung
Affine Abbildungen werden im zweidimensionelem Raum durch 2X2 Matrizen ausgedrückt. Sie haben die Form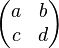 
. Für die affinen Abbildungen wichtige Rechenoperationen sind vor allem die Multiplikationen. Dabei gelten folgende Regeln:
Aufstellung einer Abbildungsmatrix
Eine Abbildungsvorschrift wird durch eine Matrix in Multiplikation mit dem Ortsvektor zu einem beliebigen Punkt, sowie einer Addition eines eventuell vorkommenden Verschiebungsvektor, vollständig beschrieben:
.
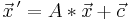Häufig finden sich Rechenaufgaben, in denen Ihnen drei beliebige Punkte und deren Bildpunkte gegeben sind. Anhand dieser Bedingungen (drei punkte und ihre Bilder) lassen sich sämtliche Abbildungen mathematisch erfassen und wird es desweiteren möglich, eine Abbildungsvorschrift zu entwickeln.
Besonders einfach ist es dabei, die gegebenen Punkte und Bildpunkte durch eine Linearkombination der Einheitsvektoren darzustellen. Es gilt: die Bilder der Einheitsvektoren entsprechen den Spaltenvektoren der Abbildungsmatrix.
allgemeines Rechenbeispiel: gegeben sind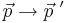 
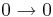
- gesucht ist die Abbildungsmatrix
