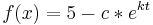Beschränktes Wachstum: Unterschied zwischen den Versionen
Aus KAS-Wiki
Julian (Diskussion | Beiträge) |
Vieth1 (Diskussion | Beiträge) |
||
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | {{#ev:youtube|WkBkppLcewE}} | ||
| + | |||
Die Änderungsrate des exponentiellen Wachstums ist proportional zur Wachstumsfunktion f(x). Die Proportionalitätskonstante ist die Wachstumskonstante k. Bei beschränktem Wachstum müssen wir nun beachten, dass eine natürliche Schranke das exponentielle Wachstum verhindert. Die Änderungsrate des beschränkten Wachstums ist proportional zu der Differenz der Schranke S von der Ausgangsfunktion f(x). Die Proportionalitätskonstante ist die Wachstumskonstante k. | Die Änderungsrate des exponentiellen Wachstums ist proportional zur Wachstumsfunktion f(x). Die Proportionalitätskonstante ist die Wachstumskonstante k. Bei beschränktem Wachstum müssen wir nun beachten, dass eine natürliche Schranke das exponentielle Wachstum verhindert. Die Änderungsrate des beschränkten Wachstums ist proportional zu der Differenz der Schranke S von der Ausgangsfunktion f(x). Die Proportionalitätskonstante ist die Wachstumskonstante k. | ||
| Zeile 12: | Zeile 14: | ||
=> | => | ||
<math>f(x)=5-c*e^{kt}</math> | <math>f(x)=5-c*e^{kt}</math> | ||
| + | |||
| + | |||
| + | [[Kategorie: Mathematik]] | ||
| + | [[Kategorie: Wachstum]] | ||
Aktuelle Version vom 9. September 2011, 19:44 Uhr
Die Änderungsrate des exponentiellen Wachstums ist proportional zur Wachstumsfunktion f(x). Die Proportionalitätskonstante ist die Wachstumskonstante k. Bei beschränktem Wachstum müssen wir nun beachten, dass eine natürliche Schranke das exponentielle Wachstum verhindert. Die Änderungsrate des beschränkten Wachstums ist proportional zu der Differenz der Schranke S von der Ausgangsfunktion f(x). Die Proportionalitätskonstante ist die Wachstumskonstante k.
f'(x)=k*(S-f(x))
Die Lösung dieser Differenzialgleichung ist:
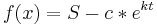
Dies kann man zum Beispiel so darstellen: Die Schranke S beträgt 5, dass heißt dass das exponentielle Wachstum nicht über den Wert von 5 hinauswächst.
f'(x)=5-f(x)
=>