Kurvendiskussion.: Unterschied zwischen den Versionen

Aus KAS-Wiki
Wechseln zu: Navigation, Suche
(→‎Grenzverhalten)
(→‎Beispiel: Aufzählung)
 
(50 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt)
Zeile 1: Zeile 1:
 +
== Beispiel Aufgabe ==
 +
 +
<math>\!f(x)=2-\frac{5}{2}x^2+x^4</math>
 +
 
== Definitionsbereich ==
 
== Definitionsbereich ==
  
 +
<math>\mathbb{D}</math>=<math>\mathbb{R}</math>
  
 
== Symmetrie ==
 
== Symmetrie ==
Zeile 16: Zeile 21:
  
 
Funktionen mit '''<u>geraden und ungeraden</u>''' Exponenten weisen <u>'''keine'''</u> Symmetrie auf.
 
Funktionen mit '''<u>geraden und ungeraden</u>''' Exponenten weisen <u>'''keine'''</u> Symmetrie auf.
 +
 +
 +
=== Beispiel ===
 +
 +
Da '''alle Exponenten''' der Funktion '''gerade''' sind, ist die Funktion '''achsensymmetrisch'''.
  
 
== Nullstellen ==
 
== Nullstellen ==
  
−
Schnittpunkte der Funktion mit der x-Achse
+
<br />Schnittpunkte der Funktion mit der x-Achse
  
 
<math> f\!(x)=0 </math>
 
<math> f\!(x)=0 </math>
 +
 +
 +
=== Beispiel ===
 +
 +
<math>\!f(x)=0</math><br /><br />
 +
<math>\!2-\frac{5}{2}x^2+x^4=0</math><br /><br />
 +
<math>\!x^4-\frac{5}{2}x^2+2=0</math><br /><br />
 +
<math>\!x^2=z</math> (Substitution)<br /><br />
 +
<math>\!z^2-\frac{5}{2}z+2=0</math><br /><br />
 +
<math>\!x_1,_2=\frac{5}{4}\pm\sqrt{\frac{25}{16}-2}</math><br /><br />
 +
<math>\!=\frac{5}{4}\pm\sqrt{\frac{25-32}{4}}</math><br /><br />
 +
<math>\!\Rightarrow</math> '''Keine Lösung''', da negative Zahl unter der Wurzel steht.
  
 
== Ableitung ==
 
== Ableitung ==
Zeile 33: Zeile 55:
  
 
<math>f\!\,''(x_0)</math> gibt die Krümmung von <math>x_0\!</math> an. <br /><br />
 
<math>f\!\,''(x_0)</math> gibt die Krümmung von <math>x_0\!</math> an. <br /><br />
−
Bei '''<u>positiven Werten</u>''' handelt es sich dabei um eine '''<u>Rechtskrümmung</u>''', bei '''<u>negativen Werten</u>''', um eine '''<u>Linkskrümmung</u>'''.
+
Bei '''<u>positiven Werten</u>''' handelt es sich dabei um eine '''<u>Linkskrümmung</u>''', bei '''<u>negativen Werten</u>''', um eine '''<u>Rechtskrümmung</u>'''.
  
  
Zeile 39: Zeile 61:
  
  
−
siehe [[Ableitungsregeln.]]
+
siehe dazu [[Ableitungsregeln.]]
 +
 
 +
 
 +
=== Beispiel ===
 +
 
 +
<math>\!f(x)=2-\frac{5}{2}x^2+x^4</math><br /><br />
 +
'''1. Ableitung'''<br /><math>\!f'(x)=-5x+4x^3</math><br /><br />
 +
'''2. Ableitung'''<br /><math>\!f''(x)=-5+12x^2</math><br /><br />
 +
'''3. Ableitung'''<br /><math>\!f'''(x)=24x</math>
  
 
== Extrempunkte ==
 
== Extrempunkte ==
  
−
In Extrempunkten (Hoch- und Tiefpunkten) ist die Steigung m=0, <br />deshalb folgt die '''notwendige Bedingung''' <math>f\!\,'(x)=0</math>
+
In Extrempunkten (Hoch- und Tiefpunkten) ist die Steigung m=0, deshalb folgt die '''notwendige Bedingung''' <math>f\!\,'(x)=0</math>
 +
 
 +
 
 +
Die erhaltenen X-Werte setzt man in der '''hinreichenden Bedingung''' in die '''zweite Ableitung''' ein. <math>\Rightarrow</math>
 +
<br /><br /><math>f\!\,''(x)>0</math> hierbei handelt es sich um eine '''<u>Linkskrümmung</u>''', also um ein '''<u>Minimum</u>''' '''(Tiefpunkt)'''.
 +
<br /><br />oder<br />
 +
<br />
 +
<math>f\!\,''(x)<0</math> hierbei handelt es sich um eine '''<u>Rechtskrümmung</u>''', also um ein '''<u>Maximum</u>''' '''(Hochpunkt)'''.
 +
<br /><br /><br />
 +
Setzt man nun die x-Werte in die Funktion <math>\!f(x)</math> ein, erhält man die y-Koordinaten der Hoch- bzw. Tiefpunkte.
 +
 
 +
 
 +
=== Beispiel ===
 +
 
 +
<br />'''Notwendige Bedingung:''' <math>\!f'(x)=0</math><br /><br />
 +
<math>\!-5x+4x^3=0</math><br /><br />
 +
<math>\!x(4x^2-5)=0</math><br /><br />
 +
<math>\!x_1=0</math><br /><br />
 +
<math>\!4x^2-5=0</math><br /><br />
 +
<math>\!4x^2=5</math><br /><br />
 +
<math>\!x^2=\frac{5}{4}</math><br /><br />
 +
<math>\!x_2,_3=\pm\sqrt{\frac{5}{4}}</math><br /><br />
 +
<math>\!x_2=1,12</math><br /><br />
 +
<math>\!x_3=-1,12</math><br /><br />
 +
'''Lösumg:''' <math>\!x_1=0</math> ; <math>\!x_2=1,12</math> ; <math>\!x_3=-1,12</math><br /><br />
 +
 
 +
'''Hinreichende Bedingung'''<br /><br />
 +
<math>\!f''(0)=-5\Rightarrow (0/2)</math>Hochpunkt<br /><br />
 +
<math>\!f''(1,12)=10,1\Rightarrow(1,12/0,438)</math>Tiefpunkt<br /><br />
 +
<math>\!f''(-1,12)=10,1\Rightarrow(-1,12/0,438)</math> Tiefpunkt
  
 
== Wendepunkte ==
 
== Wendepunkte ==
  
 +
In einem '''Wendepunkt''' wechselt die Krümmung zwischen links und rechts. Somit ist die Krümmung, die '''zweite Ableitung''' in diesem Punkt '''= 0'''.
 +
 +
<br />'''Notwedige Bedingung'''
 +
 +
<math>f\!\,''(x)=0</math>
 +
 +
<br /><br />Um zu überprüfen, ob es sich wirklich um ein Wendepunkt handelt, muss dazu auch die '''hinreichende Bedingung''' erfüllt sein.
 +
 +
<br />'''Hinreichende Bedingung'''
 +
 +
<math>f\!\,''(x)=0 \quad \vee \quad f\!\,'''(x)\not=0</math>
 +
 +
<br />Setzt man nun die x-Werte in die Funktion <math>\!f(x)</math> ein, erhält man die y-Koordinaten der Hoch- bzw. Tiefpunkte. (Wie bei den Extremwerten)
 +
 +
<br />
 +
=== Sattelpunkt ===
 +
 +
Bei einem '''Sattelpunkt''' handelt es sich um einen besonderen Wendepunkt, da es zu diesem Punkt eine '''waagerechte Tangente''' gibt. Somit ist hier die '''Steigung m=0.'''
 +
 +
 +
=== Beispiel ===
 +
 +
<br />'''Notwendige Bedingung:''' <math>\!f''(x)=0</math><br /><br />
 +
<math>\!-5+12x^2=0</math><br /><br />
 +
<math>\!12x^2=5</math><br /><br />
 +
<math>\!x^2=\frac{5}{12}</math><br /><br />
 +
<math>\!x_1,_2=\pm\sqrt{\frac{5}{12}}</math><br /><br />
 +
<math>\!x_1=\sqrt{\frac{5}{12}}</math><br /><br />
 +
<math>\!x_2=-\sqrt{\frac{5}{12}}</math><br /><br />
 +
'''Lösung:''' <math>\!x_1=\sqrt{\frac{5}{12}}</math> ; <math>\!x_2=-\sqrt{\frac{5}{12}}</math>
 +
 +
'''Hinreichende Bedingung'''
 +
 +
<math>\!f'''(\sqrt{\frac{5}{12}})=15,504\Rightarrow (0,646/1,13)</math><br /><br />
 +
<math>\!f'''(-\sqrt{\frac{5}{12}})=-15,504\Rightarrow (-0,646/1,13)</math>
  
 
== Grenzverhalten ==
 
== Grenzverhalten ==
Zeile 58: Zeile 152:
  
 
<math>\lim_{x \to -\infty}f(x)</math>
 
<math>\lim_{x \to -\infty}f(x)</math>
 +
 +
 +
=== Beispiel ===
 +
<math>\lim_{x \to \infty}f(x)=2-\frac{5}{2}x^2+x^4=\infty</math><br /><br />
 +
<math>\lim_{x \to -\infty}f(x)=2-\frac{5}{2}x^2+x^4=\infty</math>
 +
 +
== Zeichnung ==
 +
 +
 +
=== Beispiel ===
 +
 +
<math>\!f(x)=2-\frac{5}{2}x^2+x^4</math><br /><br />
 +
 +
* Funktion ist achsensymmetrisch
 +
* Keine Nullstelle
 +
* Hochpunkt in <math>\!(0/2)</math>; Tiefpunkt in <math>\!(1,12/0,438)</math> und <math>\!(-1,12/0,438)</math>
 +
* Wendepunkt in <math>\!(0,646/1,3)</math> und <math>\!(-0,646/1,3)</math>
 +
* Grenzverhalten: Funktion "kommt" aus +<math>\!\infty</math> und "geht" nach +<math>\!\infty</math>
 +
 +
 +
[[Bild:Zeichnung Kurvendiskussion.jpg]]
 +
 +
 +
[[Kategorie:Kurvendiskussion|!]]

Aktuelle Version vom 27. Dezember 2010, 10:41 Uhr

Inhaltsverzeichnis

Beispiel Aufgabe

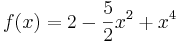
\!f(x)=2-\frac{5}{2}x^2+x^4

Definitionsbereich

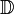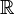
\mathbb{D}=\mathbb{R}

Symmetrie

Punktsymmetrie

f\!(-x)=-f(x)

Alle Exponenten der Funktion sind ungerade.

Achsensymmetrie

f\!(-x)=f(x)

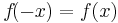
Alle Exponenten der Funktion sind gerade.


Funktionen mit geraden und ungeraden Exponenten weisen keine Symmetrie auf.


Beispiel

Da alle Exponenten der Funktion gerade sind, ist die Funktion achsensymmetrisch.

Nullstellen


Schnittpunkte der Funktion mit der x-Achse

f\!(x)=0


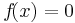
Beispiel

\!f(x)=0

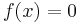
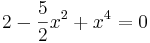
\!2-\frac{5}{2}x^2+x^4=0

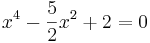
\!x^4-\frac{5}{2}x^2+2=0

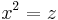\!x^2=z (Substitution)

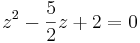
\!z^2-\frac{5}{2}z+2=0

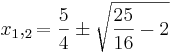
\!x_1,_2=\frac{5}{4}\pm\sqrt{\frac{25}{16}-2}

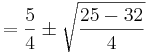
\!=\frac{5}{4}\pm\sqrt{\frac{25-32}{4}}

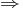\!\Rightarrow Keine Lösung, da negative Zahl unter der Wurzel steht.

Ableitung

1. Ableitung 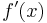f\!\,'(x)

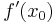f\!\,'(x_0) gibt die Steigung m im Punkt 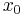x_0\! an.


2. Ableitung 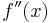f\!\,''(x)

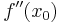f\!\,''(x_0) gibt die Krümmung von 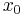x_0\! an.

Bei positiven Werten handelt es sich dabei um eine Linkskrümmung, bei negativen Werten, um eine Rechtskrümmung.


3. Ableitung 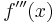f\!\,'''(x)


siehe dazu Ableitungsregeln.


Beispiel

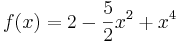
\!f(x)=2-\frac{5}{2}x^2+x^4

1. Ableitung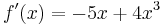
\!f'(x)=-5x+4x^3

2. Ableitung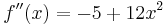
\!f''(x)=-5+12x^2

3. Ableitung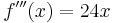
\!f'''(x)=24x

Extrempunkte

In Extrempunkten (Hoch- und Tiefpunkten) ist die Steigung m=0, deshalb folgt die notwendige Bedingung 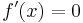f\!\,'(x)=0


Die erhaltenen X-Werte setzt man in der hinreichenden Bedingung in die zweite Ableitung ein. 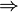\Rightarrow

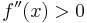f\!\,''(x)>0 hierbei handelt es sich um eine Linkskrümmung, also um ein Minimum (Tiefpunkt).

oder

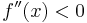f\!\,''(x)<0 hierbei handelt es sich um eine Rechtskrümmung, also um ein Maximum (Hochpunkt).


Setzt man nun die x-Werte in die Funktion 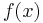\!f(x) ein, erhält man die y-Koordinaten der Hoch- bzw. Tiefpunkte.


Beispiel


Notwendige Bedingung: 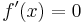\!f'(x)=0

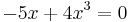
\!-5x+4x^3=0

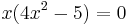
\!x(4x^2-5)=0

\!x_1=0

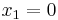
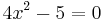
\!4x^2-5=0

\!4x^2=5

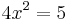
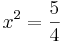
\!x^2=\frac{5}{4}

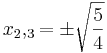
\!x_2,_3=\pm\sqrt{\frac{5}{4}}

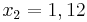
\!x_2=1,12

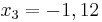
\!x_3=-1,12

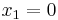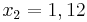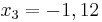
Lösumg: \!x_1=0 ; \!x_2=1,12 ; \!x_3=-1,12

Hinreichende Bedingung

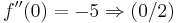\!f''(0)=-5\Rightarrow (0/2)Hochpunkt

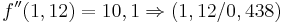\!f''(1,12)=10,1\Rightarrow(1,12/0,438)Tiefpunkt

\!f''(-1,12)=10,1\Rightarrow(-1,12/0,438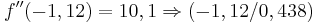) Tiefpunkt

Wendepunkte

In einem Wendepunkt wechselt die Krümmung zwischen links und rechts. Somit ist die Krümmung, die zweite Ableitung in diesem Punkt = 0.


Notwedige Bedingung

f\!\,''(x)=0



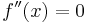
Um zu überprüfen, ob es sich wirklich um ein Wendepunkt handelt, muss dazu auch die hinreichende Bedingung erfüllt sein.


Hinreichende Bedingung

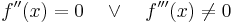
f\!\,''(x)=0 \quad \vee \quad f\!\,'''(x)\not=0


Setzt man nun die x-Werte in die Funktion 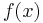\!f(x) ein, erhält man die y-Koordinaten der Hoch- bzw. Tiefpunkte. (Wie bei den Extremwerten)


Sattelpunkt

Bei einem Sattelpunkt handelt es sich um einen besonderen Wendepunkt, da es zu diesem Punkt eine waagerechte Tangente gibt. Somit ist hier die Steigung m=0.


Beispiel


Notwendige Bedingung: 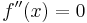\!f''(x)=0

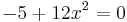
\!-5+12x^2=0

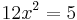
\!12x^2=5

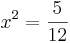
\!x^2=\frac{5}{12}

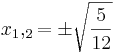
\!x_1,_2=\pm\sqrt{\frac{5}{12}}

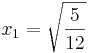
\!x_1=\sqrt{\frac{5}{12}}

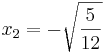
\!x_2=-\sqrt{\frac{5}{12}}

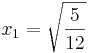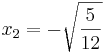
Lösung: \!x_1=\sqrt{\frac{5}{12}} ; \!x_2=-\sqrt{\frac{5}{12}}

Hinreichende Bedingung

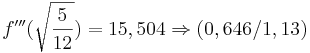
\!f'''(\sqrt{\frac{5}{12}})=15,504\Rightarrow (0,646/1,13)

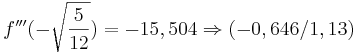
\!f'''(-\sqrt{\frac{5}{12}})=-15,504\Rightarrow (-0,646/1,13)

Grenzverhalten

Der Verlauf des Graphen bei unendlich großen bzw. unendlich kleinen x-Werten wird durch das Grenzverhalten beschrieben.


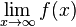
\lim_{x \to \infty}f(x)


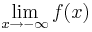
\lim_{x \to -\infty}f(x)


Beispiel

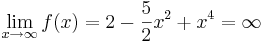
\lim_{x \to \infty}f(x)=2-\frac{5}{2}x^2+x^4=\infty

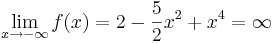
\lim_{x \to -\infty}f(x)=2-\frac{5}{2}x^2+x^4=\infty

Zeichnung

Beispiel

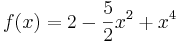
\!f(x)=2-\frac{5}{2}x^2+x^4

  • Funktion ist achsensymmetrisch
  • Keine Nullstelle
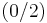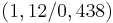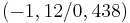
  • Hochpunkt in \!(0/2); Tiefpunkt in \!(1,12/0,438) und \!(-1,12/0,438)
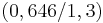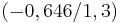
  • Wendepunkt in \!(0,646/1,3) und \!(-0,646/1,3)
  • Grenzverhalten: Funktion "kommt" aus +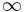\!\infty und "geht" nach +\!\infty


Zeichnung Kurvendiskussion.jpg

Von „http://kas.zum.de/index.php?title=Kurvendiskussion.&oldid=5034“