Die gleichförmige Bewegung: Unterschied zwischen den Versionen

Aus KAS-Wiki
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: „{| class = "wikitable" !Zeit in ms !/delta t^1 !/delta t !/delta t + /delta t^2 |- |1. Bewegung |- |2. Bewegung |- |3. Bewegung |- |Ortskoordinate x in cm |- |Zus…“)
 
(→‎Aufgaben)
 
(10 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt)
Zeile 1: Zeile 1:
 
{| class = "wikitable"
 
{| class = "wikitable"
 
!Zeit in ms
 
!Zeit in ms
−
!/delta t^1
+
!<math>\delta t^1</math>
−
!/delta t
+
!<math>\delta t^2</math>
−
!/delta t + /delta t^2
+
!<math>\delta t + \delta t^2</math>
 
|-
 
|-
 
|1. Bewegung
 
|1. Bewegung
 +
|0,020
 +
|0,684
 +
|0,752
 
|-
 
|-
 
|2. Bewegung
 
|2. Bewegung
 +
|0,015
 +
|0,414
 +
|0,438
 
|-
 
|-
 
|3. Bewegung
 
|3. Bewegung
 +
|0,011
 +
|0,309
 +
|0,325
 
|-
 
|-
 
|Ortskoordinate x in cm
 
|Ortskoordinate x in cm
 +
|1,0
 +
|20,0
 +
|21,0
 
|-
 
|-
 
|Zusammenhang von x und t
 
|Zusammenhang von x und t
 +
|67
 +
|48
 +
|48
 
|}
 
|}
 +
 +
 +
==Aufgaben==
 +
'''<u>Graph (Aufgabe 2,6):</u>'''
 +
 +
Bild:
 +
 +
 +
Wenn der Graph eine Gerade ist,dann ist die Bewegung gleichförmig ( Bewegung 2 und 3 ).
 +
Ist der Graph bebogen etc. dann ist die Bewegung ungleichförmig ( Beweging 1 ).
 +
 +
 +
<u>'''Aufgabe 3:'''</u>
 +
1,0 : 0,015 = 66,66666667
 +
 +
20,0 : 0,414 = 48,30917874
 +
 +
21,0 : 0,438 = 47,94520548
 +
 +
(Zusammenhang in der Tabelle)
 +
 +
 +
<u>'''Aufgabe 4:'''</u>
 +
Für uns bedeutet x:t die Ortskoordinate geteilt durch die Zeit.
 +
 +
 +
<u>'''Aufgabe 5:'''</u>
 +
Uns fällt auf, dass es immer einen Zeitunterschied von 0,2 sec gibt.
 +
 +
 +
<u>'''Aufgabe 7:'''</u>
 +
Eine Bewegung heißt gleichförmig, wenn sie gradlinig verläuft und wenn in gleichen Zeitabschnitten <math>\delta t</math> die gleichen Wegabschnitte <math>\delta s</math> zurücklegt. Das heißt, z.B wenn es eine Strecke von 20 m. gibt und das Fahrzeug braucht für 10 m. jeweils 2 Sekunden, dann ist die Bewegung gleichförmig. Wenn es einmal
 +
 +
 +
{{#ev:youtube|U5uu5KNrTBU}}
 +
 +
{{#ev:youtube|UhAsJvEnW6Q}}
 +
 +
[[Kategorie:Mechanik]]

Aktuelle Version vom 6. Juli 2011, 15:06 Uhr

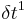
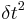
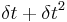
Zeit in ms \delta t^1 \delta t^2 \delta t + \delta t^2
1. Bewegung 0,020 0,684 0,752
2. Bewegung 0,015 0,414 0,438
3. Bewegung 0,011 0,309 0,325
Ortskoordinate x in cm 1,0 20,0 21,0
Zusammenhang von x und t 67 48 48


Aufgaben

Graph (Aufgabe 2,6):

Bild:


Wenn der Graph eine Gerade ist,dann ist die Bewegung gleichförmig ( Bewegung 2 und 3 ). Ist der Graph bebogen etc. dann ist die Bewegung ungleichförmig ( Beweging 1 ).


Aufgabe 3: 1,0 : 0,015 = 66,66666667

20,0 : 0,414 = 48,30917874

21,0 : 0,438 = 47,94520548

(Zusammenhang in der Tabelle)


Aufgabe 4: Für uns bedeutet x:t die Ortskoordinate geteilt durch die Zeit.


Aufgabe 5: Uns fällt auf, dass es immer einen Zeitunterschied von 0,2 sec gibt.


Aufgabe 7: Eine Bewegung heißt gleichförmig, wenn sie gradlinig verläuft und wenn in gleichen Zeitabschnitten 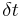\delta t die gleichen Wegabschnitte 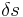\delta s zurücklegt. Das heißt, z.B wenn es eine Strecke von 20 m. gibt und das Fahrzeug braucht für 10 m. jeweils 2 Sekunden, dann ist die Bewegung gleichförmig. Wenn es einmal


Von „http://kas.zum.de/index.php?title=Die_gleichförmige_Bewegung&oldid=9789“