Ableitungsregeln.: Unterschied zwischen den Versionen
Aus KAS-Wiki
Chris1 (Diskussion | Beiträge) (→Ableitungen (Ableitungsfunktionen) spezieller Funktionen) |
K (→Differenzregel) |
||
| (7 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 49: | Zeile 49: | ||
<math>f\!(x)=g(x)-h(x)</math> | <math>f\!(x)=g(x)-h(x)</math> | ||
| − | => <math>f\!\,'(x)=g'(x)-h'( | + | => <math>f\!\,'(x)=g'(x)-h'(x)</math> |
| Zeile 56: | Zeile 56: | ||
<math>f\!(x)=x^9-x^7</math> | <math>f\!(x)=x^9-x^7</math> | ||
| − | => <math>f\!\,'(x)= (x^9)' - (x^7)' = \boldsymbol{\underline{\underline{9x^8 | + | => <math>f\!\,'(x)= (x^9)' - (x^7)' = \boldsymbol{\underline{\underline{9x^8 - 7x^6}}} </math> |
| − | + | ||
| − | + | ||
=== Produktregel === | === Produktregel === | ||
| Zeile 93: | Zeile 91: | ||
| − | |||
| − | + | ==== Beispiel 2 ==== | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| Zeile 135: | Zeile 113: | ||
<math>f\!\,'(x)=\boldsymbol{\underline{\underline{x^{n-1} \cdot e^{x} \cdot (n+x)}}}</math> | <math>f\!\,'(x)=\boldsymbol{\underline{\underline{x^{n-1} \cdot e^{x} \cdot (n+x)}}}</math> | ||
| − | |||
| − | |||
=== Quotientenregel === | === Quotientenregel === | ||
| Zeile 179: | Zeile 155: | ||
Die Ableitung von einer verketteten Funktion wird grob gesagt gebildet, indem man erst die äußere Ableitung und dann die innere bildet. | Die Ableitung von einer verketteten Funktion wird grob gesagt gebildet, indem man erst die äußere Ableitung und dann die innere bildet. | ||
| − | ==== Beispiel | + | ==== Beispiel ==== |
<math>f\!(x) = (x^2 + 2x)^2</math> <br /> | <math>f\!(x) = (x^2 + 2x)^2</math> <br /> | ||
<math>f\! '(x) = 2(x^2 + 2x)*(2x + 2) </math> | <math>f\! '(x) = 2(x^2 + 2x)*(2x + 2) </math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==== Hilfestellung ==== | ==== Hilfestellung ==== | ||
| Zeile 194: | Zeile 165: | ||
<math>f\! '(x) = u'(v(x)) * v'(x)</math> | <math>f\! '(x) = u'(v(x)) * v'(x)</math> | ||
| − | '''Beispiel von oben | + | '''Beispiel von oben:''' |
| + | <math>f\! (x) = (x^2 + 2x)^2</math> | ||
| − | <math> | + | <math>u\! = ()^2</math><math>u\! ' = 2()</math> <br /> |
| + | <math>v\! = x^2+2x </math><math>v\! ' = 2x+2</math> | ||
| − | |||
| − | |||
| − | + | <math>f\! '(x) =2(x^2 + 2x)*(2x + 2) </math><br /> | |
| − | <math>f\! '(x) = | + | |
Also: <math>f\! '(x) = u' (v(x)) * v'(x)</math> | Also: <math>f\! '(x) = u' (v(x)) * v'(x)</math> | ||
=== Umkehrregel === | === Umkehrregel === | ||
| − | <math> | + | <math>x=g(y)\ Umkehrfunktion\ von\ y=f(x)</math> |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| + | <math>=>\ g'(y)= \frac{1}{f'(x)}</math> | ||
=== Ableitungen (Ableitungsfunktionen) spezieller Funktionen === | === Ableitungen (Ableitungsfunktionen) spezieller Funktionen === | ||
| Zeile 245: | Zeile 210: | ||
| <math>\!a^x*ln\ a</math> | | <math>\!a^x*ln\ a</math> | ||
| <math>\!a^x*(ln\ a)^2</math> | | <math>\!a^x*(ln\ a)^2</math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|- | |- | ||
| <math>\! log_a x</math> | | <math>\! log_a x</math> | ||
| Zeile 267: | Zeile 220: | ||
|- | |- | ||
|} | |} | ||
| + | |||
| + | [[Kategorie:Funktionen]] | ||
Aktuelle Version vom 9. Dezember 2013, 10:33 Uhr
Inhaltsverzeichnis[Verbergen] |
Ableitungsregeln
Potenzregel
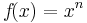
=> 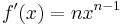
Beispiel
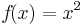
=> 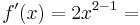
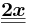
Summenregel
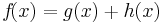
=> 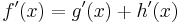
Beispiel
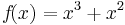
=> 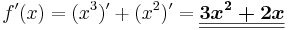
Faktorregel
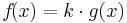
=> 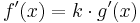
Beispiel
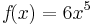
=> 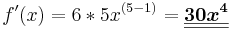
Differenzregel
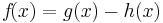
=> 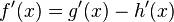
Beispiel
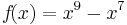
=> 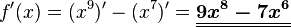
Produktregel
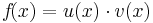
=> 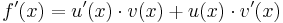
Beispiel 1
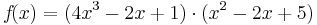
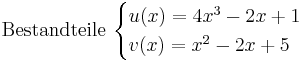
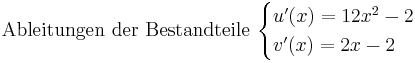
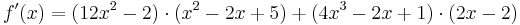
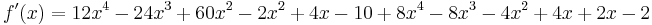
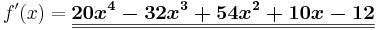
Beispiel 2
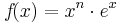
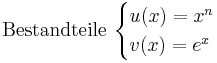
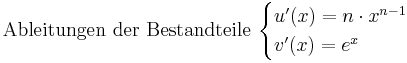
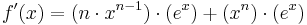
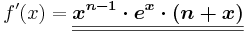
Quotientenregel
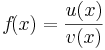
=> 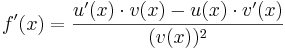
Beispiel
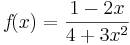
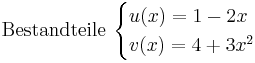
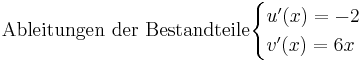
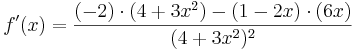
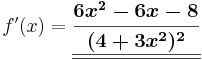
Kettenregel
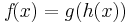 bzw.
bzw.  mit
mit 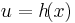
=> 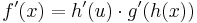
Die Ableitung von einer verketteten Funktion wird grob gesagt gebildet, indem man erst die äußere Ableitung und dann die innere bildet.
Beispiel
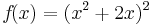
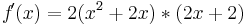
Hilfestellung
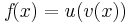
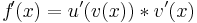
Beispiel von oben:
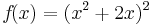
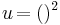
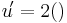
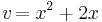
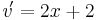
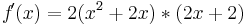
Also: 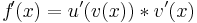
Umkehrregel
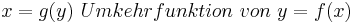
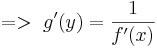
Ableitungen (Ableitungsfunktionen) spezieller Funktionen
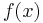
|
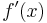
|
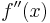
|
|---|---|---|
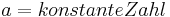
|
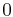
|
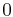
|
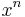
|
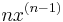
|
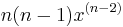
|
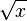
|
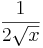
|
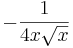
|
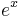
|
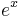
|
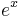
|
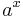
|
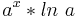
|
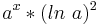
|
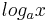
|
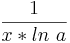
|
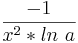
|
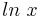
|
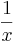
|
|

