Auswertung: Unterschied zwischen den Versionen
Belgin (Diskussion | Beiträge) |
Belgin (Diskussion | Beiträge) |
||
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
== Auswertung == | == Auswertung == | ||
<br /><br />Wir betrachten die drei Bewegungen des Messwagens jeweils von der Fahrbahnmarke<br /> 0 aus und lassen die Zeitrechnung bei null beginnen, wenn die vordere Kante des Messaufsatzes die Fahrbahnmarke 0 passiert.<br /> Nach der Zeit <math>\delta</math>t1 hat sie dann dieOrtskoordinate 1,0 ( Durchmesser der Messaufsatzes),<br /> nach der Zeit <math>\delta</math>t die Ortskoordinate 20,0 und nach der Zeit <math>\delta</math>t+<math>\delta</math>t2 die Ortskoordinate 21,0.<br /><br /> | <br /><br />Wir betrachten die drei Bewegungen des Messwagens jeweils von der Fahrbahnmarke<br /> 0 aus und lassen die Zeitrechnung bei null beginnen, wenn die vordere Kante des Messaufsatzes die Fahrbahnmarke 0 passiert.<br /> Nach der Zeit <math>\delta</math>t1 hat sie dann dieOrtskoordinate 1,0 ( Durchmesser der Messaufsatzes),<br /> nach der Zeit <math>\delta</math>t die Ortskoordinate 20,0 und nach der Zeit <math>\delta</math>t+<math>\delta</math>t2 die Ortskoordinate 21,0.<br /><br /> | ||
| + | |||
(1) Trage die Messwerte für die 2. Bewegung in ein x-t- Diagramm ein und verbinde sie zu einem sinnvollen Graph.<br /> Wähle hierzu günstige Einheiten, vor allem für die Zeitachse, um auch die Graphen für die beiden anderen<br /> Bewegungen vollständig aufnehmen können. | (1) Trage die Messwerte für die 2. Bewegung in ein x-t- Diagramm ein und verbinde sie zu einem sinnvollen Graph.<br /> Wähle hierzu günstige Einheiten, vor allem für die Zeitachse, um auch die Graphen für die beiden anderen<br /> Bewegungen vollständig aufnehmen können. | ||
| Zeile 16: | Zeile 17: | ||
der Quotient x:!? (falls Du mit dieser Frage nichts | der Quotient x:!? (falls Du mit dieser Frage nichts | ||
anfangen kannst, betrachte die einheit dieses Quotienten) | anfangen kannst, betrachte die einheit dieses Quotienten) | ||
| + | |||
(5) wähle im Diagramm wilkürlich drei Wegabschnitte von 1cm und ermittle aus dem Graph die entsprechenden Zeitabschnitte. Was fällt dir auf? | (5) wähle im Diagramm wilkürlich drei Wegabschnitte von 1cm und ermittle aus dem Graph die entsprechenden Zeitabschnitte. Was fällt dir auf? | ||
| + | |||
(6) Zeichne jetzt auch die Graphen für die beiden anderen Bewegungen des Wagens in das Diagramm ein, überlege aber zuvor, ob sie steiler oder flacher verlaufen als der Graph für die 2. Bewegung. | (6) Zeichne jetzt auch die Graphen für die beiden anderen Bewegungen des Wagens in das Diagramm ein, überlege aber zuvor, ob sie steiler oder flacher verlaufen als der Graph für die 2. Bewegung. | ||
| + | |||
(7) Fasse deine Ergebnisse zusammen,indem du den folgenden Text ergänzt. Gehe dabei auf die gleichen Wegabschnitte ein sowie auf den Graph und seine Steigung. | (7) Fasse deine Ergebnisse zusammen,indem du den folgenden Text ergänzt. Gehe dabei auf die gleichen Wegabschnitte ein sowie auf den Graph und seine Steigung. | ||
Eine Bewegung heißt gleichförmig, wenn sie geradelinig verläuft und ... | Eine Bewegung heißt gleichförmig, wenn sie geradelinig verläuft und ... | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Zu (4) X:t bedeutet für uns, dass die Länge der Strecke durch die benötigte Zeit geteilt wird; das heißt: die Strecke steht im Verhältnis zur Zeit. | ||
| + | |||
| + | Zu (5) Es fällt auf, dass das Fahrzeug für die Strecke von 1cm immer 0,25 Sekunden benötigt. (gleichförmig) | ||
| + | |||
| + | Zu (6) siehe Graphen | ||
| + | |||
| + | Zu (7) Eine Bewegung heißt gleichförmig, wenn sie geradelinig verläuft und steigt. dei gleichförmige Bewegung ist abhängig von der Ortskoordinate und der zeitmesspunkte. Jene können unterschiedlich hoch, schnell und langsam sein. | ||
| + | (<math>\delta</math>t, <math>\delta</math>t1, <math>\delta</math>t2, ...) | ||
Aktuelle Version vom 11. Juli 2011, 20:24 Uhr
Auswertung
Wir betrachten die drei Bewegungen des Messwagens jeweils von der Fahrbahnmarke
0 aus und lassen die Zeitrechnung bei null beginnen, wenn die vordere Kante des Messaufsatzes die Fahrbahnmarke 0 passiert.
Nach der Zeit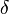 
t1 hat sie dann dieOrtskoordinate 1,0 ( Durchmesser der Messaufsatzes),
nach der Zeit 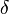t die Ortskoordinate 20,0 und nach der Zei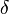t t+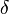t2 die Ortskoordinate 21,0.
(1) Trage die Messwerte für die 2. Bewegung in ein x-t- Diagramm ein und verbinde sie zu einem sinnvollen Graph.
Wähle hierzu günstige Einheiten, vor allem für die Zeitachse, um auch die Graphen für die beiden anderen
Bewegungen vollständig aufnehmen können.
(2) Welchen mathematischen Zusammenhang zwischen der Ortskoordinate x und der Zeit t folgerst Du aus dem Graph?
Gib eine Gleichung an.
(3) den Zusammenhang zwischen x und t kann man auch durch Rechnung erhalten. Berechne hierzu die Quotienten x:t für die 2. Bewegung auf zwei geltende Ziffern und trage sie in die unterste Zeile der Tabelle ein.
(4) Welche physikalische Bedeutung hat deiner Meinung nach
der Quotient x:!? (falls Du mit dieser Frage nichts
anfangen kannst, betrachte die einheit dieses Quotienten)
(5) wähle im Diagramm wilkürlich drei Wegabschnitte von 1cm und ermittle aus dem Graph die entsprechenden Zeitabschnitte. Was fällt dir auf?
(6) Zeichne jetzt auch die Graphen für die beiden anderen Bewegungen des Wagens in das Diagramm ein, überlege aber zuvor, ob sie steiler oder flacher verlaufen als der Graph für die 2. Bewegung.
(7) Fasse deine Ergebnisse zusammen,indem du den folgenden Text ergänzt. Gehe dabei auf die gleichen Wegabschnitte ein sowie auf den Graph und seine Steigung.
Eine Bewegung heißt gleichförmig, wenn sie geradelinig verläuft und ...
Zu (4) X:t bedeutet für uns, dass die Länge der Strecke durch die benötigte Zeit geteilt wird; das heißt: die Strecke steht im Verhältnis zur Zeit.
Zu (5) Es fällt auf, dass das Fahrzeug für die Strecke von 1cm immer 0,25 Sekunden benötigt. (gleichförmig)
Zu (6) siehe Graphen
Zu (7) Eine Bewegung heißt gleichförmig, wenn sie geradelinig verläuft und steigt. dei gleichförmige Bewegung ist abhängig von der Ortskoordinate und der zeitmesspunkte. Jene können unterschiedlich hoch, schnell und langsam sein.
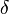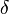(t, t1, 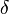t2, ...)
