PH-Wert Abhängigkeit von Redoxsystemen: Unterschied zwischen den Versionen

Aus KAS-Wiki
Wechseln zu: Navigation, Suche
Zeile 24: Zeile 24:
 
<br />
 
<br />
 
<math>E = 1,51V + 0,012V \lg \frac {1*(10^{-1})^{8}}{1} = 1,46V</math>
 
<math>E = 1,51V + 0,012V \lg \frac {1*(10^{-1})^{8}}{1} = 1,46V</math>
 +
<br />
 +
<br />
 +
Man sieht nun, dass sich das Potential um <math>\Delta E = 0,24 V </math> verändert hat.

Version vom 15. Dezember 2009, 13:25 Uhr

Das Elektrodenpotential von Redoxpaaren in sauren oder basischen Millieus hängt zusätzlich noch von dem pH-Wert des Redoxsystems ab. Diese Beziehung zwischen dem pH-Wert und dem Elektrodenpotential kann man ebenfalls durch die Nernst-Gleichung aufzeigen. Dazu betrachtet man beispielhaft die folgende Reaktion in saurem Millieu:

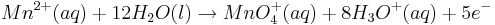
Mn^{2+}(aq) + 12 H_{2}O(l) \rightarrow MnO^{+}_{4}(aq) + 8H_{3}O^{+}(aq) + 5e^{-}

Steigt nun in diesem Beispiel die Konzentration der Oxonium-Ionen, so wird auch das Elektrodenpotential des Redoxpaares 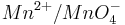Mn^{2+} / MnO^{-}_{4} steigen.
Denn formuliert man für dieses Redoxpaar die Nernst-Gleichung, so ergibt sich:

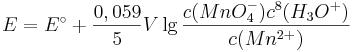
E = E^\circ + \frac {0,059}{5} V \lg \frac {c(MnO^{-}_{4})c^{8}(H_{3}O^{+})}{c(Mn^{2+})}

Setzt man nun voraus, dass die Konzentration der 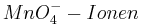MnO^{-}_{4}-Ionen und die Konzentration der 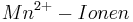Mn^{2+}_{ }-Ionen konstant bleibt, so ergibt sich bei einem pH-Wert von 3 folgendes Eregebnis für das Elektrodenpotential:


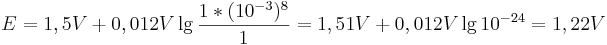
E = 1,5 V + 0,012 V \lg \frac {1 * (10^{-3})^{8}}{1} = 1,51V +0,012V \lg 10^{-24} = 1,22V

Vergleicht man diesen Wert mit einer Reaktion bei pH-Wert 1, so ergibt sich nach der Nernst-Gleich ein Potential von:


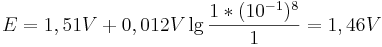
E = 1,51V + 0,012V \lg \frac {1*(10^{-1})^{8}}{1} = 1,46V

Man sieht nun, dass sich das Potential um 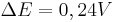\Delta E = 0,24 V verändert hat.

Von „http://kas.zum.de/index.php?title=PH-Wert_Abhängigkeit_von_Redoxsystemen&oldid=1168“