G2: Die Normalparabel: Unterschied zwischen den Versionen
Aus KAS-Wiki
(→Eigenschaften des Grafen) |
(→Eigenschaften des Grafen) |
||
| Zeile 8: | Zeile 8: | ||
Ihr Scheitelpunkt liegt bei '''(0;0)'''und die Parabel ist nach oben geöffnet, dies ist gleich zeitig <br />der Tiefpunkt der Parabel.<br /> | Ihr Scheitelpunkt liegt bei '''(0;0)'''und die Parabel ist nach oben geöffnet, dies ist gleich zeitig <br />der Tiefpunkt der Parabel.<br /> | ||
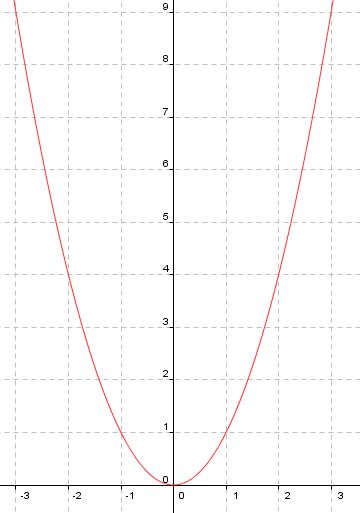
[[Bild:Normalparabel-Wertetabelle.jpg]]<br /> | [[Bild:Normalparabel-Wertetabelle.jpg]]<br /> | ||
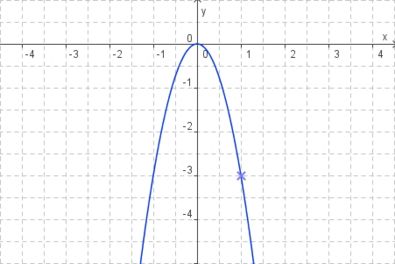
| − | Bei der Normalparabel mit der Formel '''f(x)=(-x)²''' ist die Parabel zwar symetrisch zur <br />y-Achse, jedoch ist sie nach unten geöffnet. | + | Bei der Normalparabel mit der Formel '''f(x)=(-x)²''' ist die Parabel zwar symetrisch zur <br />y-Achse, jedoch ist sie nach unten geöffnet.<br /> |
| + | [[Bild:395px-Üb1_Parabel2.jpg]]<br /> | ||
Version vom 16. Dezember 2009, 10:22 Uhr
Normalparabel
Formel
f(x)=x² und f(x)=(-x)²
Eigenschaften des Grafen
Die Normalparabel mit der Formel f(x)=x² ist immer symetrisch zur y-Achse.
Ihr Scheitelpunkt liegt bei (0;0)und die Parabel ist nach oben geöffnet, dies ist gleich zeitig
der Tiefpunkt der Parabel.
Bei der Normalparabel mit der Formel f(x)=(-x)² ist die Parabel zwar symetrisch zur
y-Achse, jedoch ist sie nach unten geöffnet.