G3: Verschobene Normalparabeln der Form f(x)=x²+e: Unterschied zwischen den Versionen
(→Defintion) |
(→Die Formeln) |
||
| Zeile 13: | Zeile 13: | ||
Es gibt zwei Möglichkeiten diese verschobene Normalparabel darzustellen: Die Formel, bei welcher, der Scheitelpunkt im positiven Bereich liegt, lautet f(x)=x²'''+'''e; die Formel, bei welcher, der Scheitelpunkt im negativen Bereich liegt, lautet f(x)=x²'''-'''e. | Es gibt zwei Möglichkeiten diese verschobene Normalparabel darzustellen: Die Formel, bei welcher, der Scheitelpunkt im positiven Bereich liegt, lautet f(x)=x²'''+'''e; die Formel, bei welcher, der Scheitelpunkt im negativen Bereich liegt, lautet f(x)=x²'''-'''e. | ||
| + | |||
| + | |||
| + | === Quellen === | ||
| + | |||
| + | |||
| + | ''Elemente der Mathematik 9'' | ||
| + | |||
| + | http://www.schule-studium.de/Mathe/Quadratische_Funktonen.html | ||
Version vom 18. Dezember 2009, 13:53 Uhr
Inhaltsverzeichnis |
Verschobene Normalparabel der Form f(x)=x²+e
Defintion
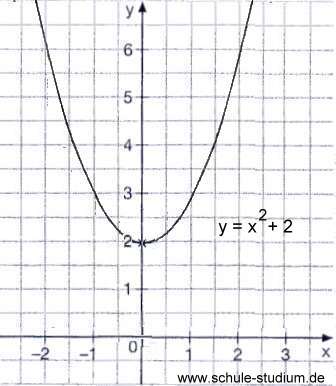
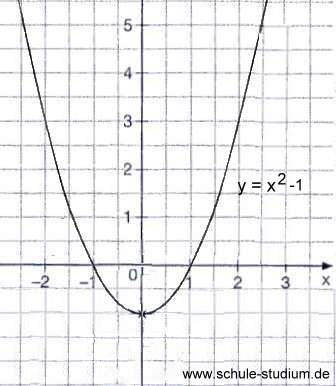
Die verschobene Normalparabel der Form f(x)=x²+e unterscheidet sich von der Normalparbel ( f(x)=x² ) durch den Faktor "e", welcher die Position des vertikal verschobenen Scheitelpunktes auf der y-Achse angibt. Ist der Faktor "e" größer als 0, so befindet sich der Scheitelpunkt der Parabel im positiven Bereich der y-Achse; ist der Faktor "e" kleiner als 0, so befindet sich der Scheitelpunkt im negativen Bereich der y-Achse. Der Graph der Funktion f(x)=x²+e ist deckungsgleich zur Normalform, das bedeutet er hat die y-Achse als Symmetrieachse und der Scheitelpunkt S(0/e). Die Normalparabel dieser Form ist immer nach oben geöffnet.
Die Formeln
Es gibt zwei Möglichkeiten diese verschobene Normalparabel darzustellen: Die Formel, bei welcher, der Scheitelpunkt im positiven Bereich liegt, lautet f(x)=x²+e; die Formel, bei welcher, der Scheitelpunkt im negativen Bereich liegt, lautet f(x)=x²-e.
Quellen
Elemente der Mathematik 9
http://www.schule-studium.de/Mathe/Quadratische_Funktonen.html