G5: Verschobene Normalparabeln der Form f(x)=(x-d)²: Unterschied zwischen den Versionen
| Zeile 42: | Zeile 42: | ||
[[Bild:Parabelnd.jpg]] | [[Bild:Parabelnd.jpg]] | ||
| − | 1) f(x)=(x+3,5)² | + | 1) f(x)=(x+3,5)² |
| − | 2) f(x)=(x+5)² | + | 2) f(x)=(x+5)² |
| − | 3) f(x)=(x-2)² | + | |
| − | 4) f(x)=(x-6)² | + | 3) f(x)=(x-2)² |
| + | 4) f(x)=(x-6)² | ||
Version vom 18. Dezember 2009, 14:18 Uhr
Da sind wir wieder, die rumreichen Genies der Mathematik! Heute werden wir Euch etwas über:
"Verschobene Normalparabeln der Form f(x)=(x-d)²" erzählen!
Und heeey, schämt Euch nicht! Wir und die Mathematik lieben Euch und Ihr greift das!!!! Toi, Toi, Toi! _______________________________________________________________________________
Der Graph einer Funktion f mit f(x)=(x-d)² erhält man durch Verschiebung der Normalparabel in Richtung der x-Achse.
Wenn d>0, wird nach rechts verschoben; wenn d<0, wird nach links verschoben.
Der Graph der Funktion f ist kongruent (siehe "Kongruenz": http://de.wikipedia.org/wiki/Kongruenz_(Geometrie))
zur Normalparabel und hat S(d/0) als Scheitelpunkt.
Die Parabel zur y-Achse mit der Gleichung x=d ist Symmetrieachse des Graphen von f.
Es gilt:
Bei:
f(x)= (x-d)² --> POSTIV! - -> +
f(x)= (x+d)² --> NEGATIV! + -> -
Ein paar Veranschaulichungen in Form von Beispielen ;):
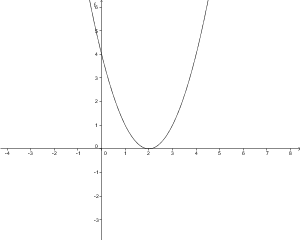
f(x)= (x-2)²
Bestimmung der Lösungsmenge:
Beispiel:
(x-2)²=9
x-2=3 oder x-2=-3
x=5 oder x=-1
L=(-1/5)
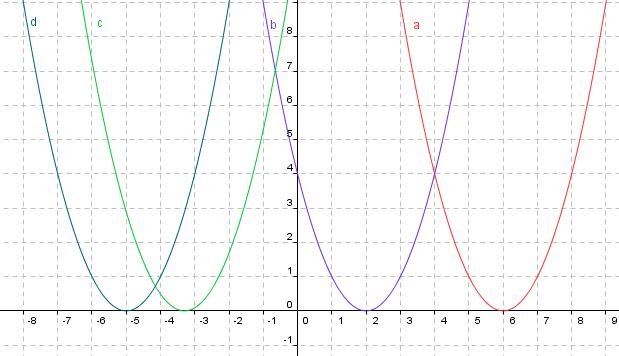
Übung zum Erkennen von verschobenen Normalparabeln:
1) f(x)=(x+3,5)² 2) f(x)=(x+5)²
3) f(x)=(x-2)² 4) f(x)=(x-6)²
Seiten die Euch beim Üben weiterhelfen: :-)
www.bartberger.de/Klasse8/mathe/quadratfuntionen/funktion_fx_x_d_wertetabelle.html
ne.lo-net2.de/selbstlernmaterial/
www.mathe1.de/mathematikbuch/funktionen_verschobenenormalparabel_31.htm
Bei Fragen, falls der Mathelehrer gerade nicht zur Stelle ist und ihr niemanden zum Erklären habt:
www.matheboard.de/
So jetzt seid Ihr hoffentlich schlauer denn je, und wie gesagt:
=== Du suchst den Kick?Willst sein ein Hot Chick?Die einzige die dir helfen kann ist, die MATHEMATIK! ===!