Gebrochene rationale Funktionen.: Unterschied zwischen den Versionen
Anabel (Diskussion | Beiträge) |
Anabel (Diskussion | Beiträge) |
||
| Zeile 71: | Zeile 71: | ||
Bei der Funktion <math>f(x)= \frac{(x+1)(x-2)}{(x+1)^2(x-2)}</math> ; D = <math>\R {-1;2}</math> sind an der Stelle <math>x_0 = -1 </math> und <math> x_1 = 2 </math> sowohl der Nenner als auch der Zähler gleich null. Nach dem Kürzen gilt: | Bei der Funktion <math>f(x)= \frac{(x+1)(x-2)}{(x+1)^2(x-2)}</math> ; D = <math>\R {-1;2}</math> sind an der Stelle <math>x_0 = -1 </math> und <math> x_1 = 2 </math> sowohl der Nenner als auch der Zähler gleich null. Nach dem Kürzen gilt: | ||
| − | Für alle x <math> \in </math> D ist <math> f(x) = \frac{1}{x+1}</math> und damit <math> \ | + | |
| + | Für alle x <math> \in </math> D ist <math> f(x) = \frac{1}{x+1}</math> und damit <math>\ lim _ {x \to \2}</math><math>f(x) = \frac{1}{3} </math> ; <math>x_1 = 2</math> ist keine Polstelle ; dort ist eine '''hebbare Definitionslücke'''. | ||
| + | <math>x_0 = -1 </math> ist eine Polstelle. An der Stelle <math>x_0 = -1 </math> hat der Graph eine '''senkrechte Asymptote''', der Punkt P ( 2 / <math>\frac{1}{3}</math> gehört nicht zum Graphen der Funktion f. | ||
Version vom 20. Dezember 2009, 12:34 Uhr
Inhaltsverzeichnis |
Defition von gebrochenrationalen Funktionen
Eine gebrochenrationale Funtion ist ein Bruch zweier ganzrationaler Funtionen g(x) und h(x). Dabei heißt g(x) Zählerfunktion mit dem Zählergrad ZG und h(x) heißt Nennerfunktion mit dem Nennergrad NG.
Allgemeine Form der Funktion: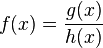 
mit dem ganzrationalen Funktionen
g(x) und h(x) ( Grad h(x) 
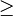1).
Bei einer ganzrationalen ist der Funktionsterm ein Polynom.
Ist z.B. g(x) =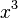 
+ x und 
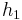(x) =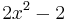 
, ergibt sich 
=
= 
.
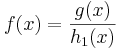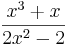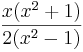Diese Art von Funktionen nennt man gebrochenrationale Funktion.
Ist dagegen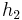 
= 
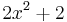, ergibt sich 
= 
= 
=
.
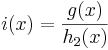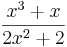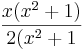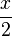Durch das Kürzen ändert sich in diesem Fall die Definitionsmende nicht. Es ergibt sich als Nennerpolynom eine Konstante. Die Funktion i ist also ein ganzrationale Funktion.
Damit kann man formulieren:
Eine Funktion f mit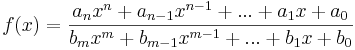 
, 
, 
, 
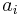
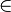
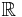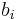
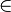
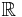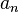
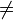0 ,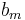 
0, heißt gebrochenrational, wenn diese Darstellung nur mit einem Nennerpolynom möglich ist, dessen Grad mindestens 1 ist.
Falls das Nennerpolynom den Grad 0 hat, ist f eine ganzrationale Funktion.
Definitionsmenge
Nenner = 0 setzen
y-Achsenabschnitt
x = 0 setzen, f(0)= ...
Nullstellen und Polstellen
Um einen Überblick über den Verlauf des Graphen einer gebrochenrationalen Funktion f mit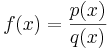 
zu gewinnen, untersucht man f zunächst auf Nullstellen des Zählers und auf Definitionslücken.
Nullstellen
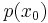= 0 und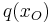 
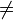0
Zähler = 0 setzen
Beispiel 1:
Bei der Funktion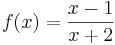 
ist an der Stelle 
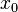= 1 der Zähler null und der Nenner ungleich null. 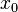ist die Nullstelle der gebrochenrationalen Funktion f.
Polstelle
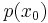
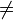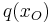0 und = 0
Nenner = 0 setzen
Beispiel 2:
Bei der Funktion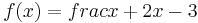 
ist an der Stelle 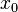= 3 der Zähler ungleich null und der Nenner null. 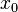ist Pollstelle der der gebrochenrationalen Funktion f.
Hebbare Definitionslücke
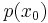= 0 und 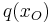= 0
Zähler und Nenner = 0
Beispiel 3:
Bei der Funktion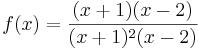 
; D =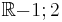 
sind an der Stelle 
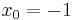und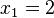 
sowohl der Nenner als auch der Zähler gleich null. Nach dem Kürzen gilt:
Für alle x 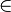D ist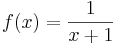 
und damit Fehler beim Parsen(Lexikalischer Fehler): \ lim _ {x \to \2}
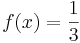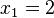; ist keine Polstelle ; dort ist eine hebbare Definitionslücke.
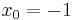ist eine Polstelle. An der Stelle 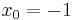hat der Graph eine senkrechte Asymptote, der Punkt P ( 2 / 
gehört nicht zum Graphen der Funktion f.
Symmetrie
a) Achsensymmetrie zur y- Achse
Bed. f(-x) = f(x)
b) Punktsymmetrie zum Ursprung
Bed. - f(-x) = f(x)
