G4: Verschobene Normalparabeln der Form f(x)=x²+e: Unterschied zwischen den Versionen
| Zeile 23: | Zeile 23: | ||
| − | Die verschobene Normalparabel kann sowohl in den | + | Die verschobene Normalparabel kann sowohl in den '''positiven''' wie auch in den '''negativen Bereich''' verschoben werden. |
| − | Wenn '''e negativ ''' ist so wird die Parabel in den '''negativen | + | Wenn '''e negativ ''' ist so wird die Parabel in den '''negativen Bereich''' der Y-Achse verschoben. |
Wenn '''e positv '''ist so wird die Parabel nach '''oben''' auf der Y-Achse verschoben. | Wenn '''e positv '''ist so wird die Parabel nach '''oben''' auf der Y-Achse verschoben. | ||
Version vom 27. Dezember 2009, 12:16 Uhr
Verschobene Normalparabel der Form f(x)=x²+e
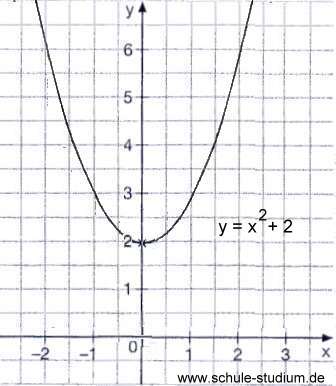
Die verschobene Normalparabel der Form "f(x)=x²+e" ist auf der Y-Achse verschoben.
Sie ist nach oben verschoben wenn e>0 ist und nach unten verschoben wenn e<0 ist.
links: Die normalparbel ist um 2 nach oben auf der Y-Achse verschoben
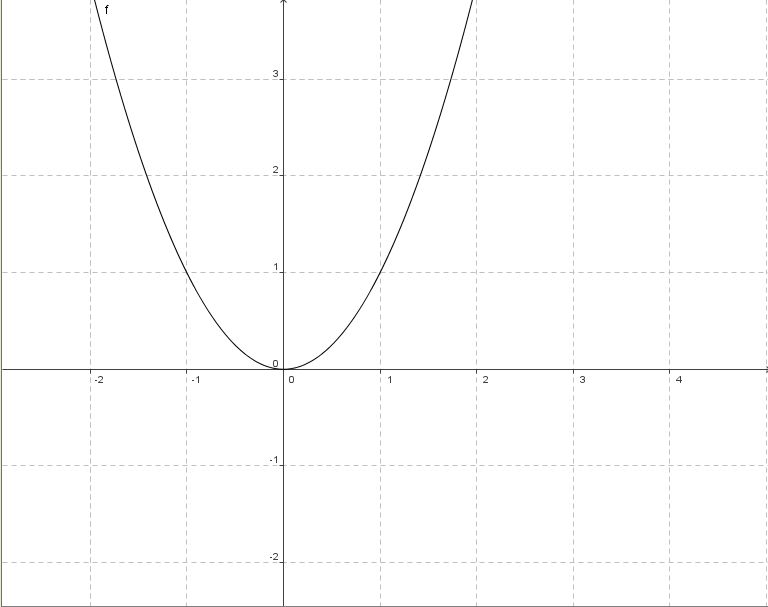
rechts: Das ist eine Normalparabel
Die verschobene Normalparabel:
Symmetrieachse: y-Achse Symmetrieachse: y
Scheitelpunkt: S(0/e)
Die verschobene Normalparabel der Form f(x)= X²+e ist immer nach oben geöffnet
Die verschobene Normalparabel kann sowohl in den positiven wie auch in den negativen Bereich verschoben werden.
Wenn e negativ ist so wird die Parabel in den negativen Bereich der Y-Achse verschoben.
Wenn e positv ist so wird die Parabel nach oben auf der Y-Achse verschoben.
Quellen
- http://www.mathe1.de/mathematikbuch/funktionen_verschobenenormalparabel_31.htm : Formel
- http://www.schule-studium.de/Mathe/Quadratische_Funktonen.html : Bilder
- Klett Elemente der Mathematik Klasse 9 : Scheitelpunkt, Symetrieachse und Parabeln generell
- http://www.youtube.com/watch?v=kakHJvnjjFo
Zum Üben!!
- http://www.tiburski.de/cybernautenshop/virtuelle_schule/dfu/quadratische_funktionen/index2.html (erste aufgabe b = e)
- http://klassenarbeiten.de 9. Klasse mathe arbeit 7b (7. Aufgabe)