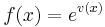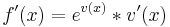Exponentialfunktionen: Unterschied zwischen den Versionen
Aus KAS-Wiki
| Zeile 1: | Zeile 1: | ||
| − | Die Exponentialfunktion beschreibt Vorgänge wie sie beispielsweise bei Verzinsung, dem Wachstum von Populationen oder radioaktivem Zerfall vorkommen.<br /> | + | Die Exponentialfunktion beschreibt Vorgänge wie sie beispielsweise bei Verzinsung, dem Wachstum von Populationen oder radioaktivem Zerfall vorkommen. Exponentialfunktionen werden deshalb auch oft Wachstums- oder Zerfallsfunktionen genannt.<br /> |
<math>x\mapsto b*a^x</math><br /> | <math>x\mapsto b*a^x</math><br /> | ||
<math>a>0; a\not=0; b\in \mathbb{R}</math> | <math>a>0; a\not=0; b\in \mathbb{R}</math> | ||
| − | Jede Exponentialfunktion lässt sich in der Form <math>\!f(x)=e^{xlna}</math> darstellen.<br /> | + | Jede Exponentialfunktion lässt sich in der Form <math>\!f(x)=e^{xlna}</math> darstellen. Dabei bezeichnet <math>\!e</math> die eulersche Zahl. <math>\!e=2,71828...</math><br /> |
Zur Erinnerung: <math>\!lna=x</math> und <math>\!e^x=a</math>. Es gilt also <math>\!e^{lna}=a</math> und damit <math>\!a^x=e^{xlna}</math>. | Zur Erinnerung: <math>\!lna=x</math> und <math>\!e^x=a</math>. Es gilt also <math>\!e^{lna}=a</math> und damit <math>\!a^x=e^{xlna}</math>. | ||
| Zeile 12: | Zeile 12: | ||
Stammfunktion:<math>\!F(x)=e^x</math><br /> | Stammfunktion:<math>\!F(x)=e^x</math><br /> | ||
Erste Ableitung:<math>\!f'(x)=e^x</math><br /> | Erste Ableitung:<math>\!f'(x)=e^x</math><br /> | ||
| + | |||
| + | Bei einer Verkettung von Funktionen mit Exponentialfunktionen wird die Kettenregel angewand.<br /> | ||
| + | <math>\!f(x)=e^{v(x)}</math><br /> | ||
| + | <math>\!f'(x)=e^{v(x)}*v'(x)</math> | ||
===Beispiele=== | ===Beispiele=== | ||
Version vom 3. Dezember 2009, 11:14 Uhr
Die Exponentialfunktion beschreibt Vorgänge wie sie beispielsweise bei Verzinsung, dem Wachstum von Populationen oder radioaktivem Zerfall vorkommen. Exponentialfunktionen werden deshalb auch oft Wachstums- oder Zerfallsfunktionen genannt.
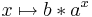
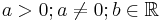Jede Exponentialfunktion lässt sich in der Form 
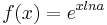darstellen. Dabei bezeichnet 
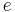die eulersche Zahl.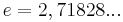 
Zur Erinnerung: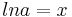 
und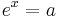 
. Es gilt also 
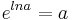und damit 
.
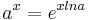Eigenschaften
Ableiten
Funktion: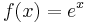
Stammfunktion: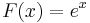
Erste Ableitung: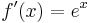
Bei einer Verkettung von Funktionen mit Exponentialfunktionen wird die Kettenregel angewand.
