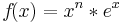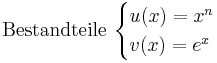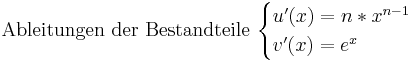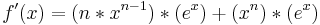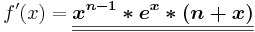Ableitungsregeln: Unterschied zwischen den Versionen
Aus KAS-Wiki
| Zeile 140: | Zeile 140: | ||
<math>f\!\,'(x)=(n*x^{n-1})*(e^{x})+(x^n)*(e^{x})</math> | <math>f\!\,'(x)=(n*x^{n-1})*(e^{x})+(x^n)*(e^{x})</math> | ||
| − | <math>f\!\,'(x)=\boldsymbol{\underline{\underline{x^{n-1}*e^{x} | + | <math>f\!\,'(x)=\boldsymbol{\underline{\underline{x^{n-1}*e^{x}*(n+x)}}}</math> |
Version vom 3. Dezember 2009, 10:16 Uhr
Inhaltsverzeichnis |
Ableitungsregeln
Potenzregel
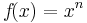
=> 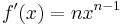
Summenregel
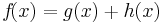
=> 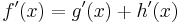
Faktorregel
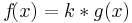
=> 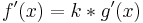
Differenzregel
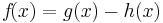
=> 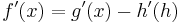
Produktregel
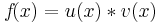
=> 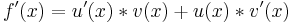
Quotientenregel
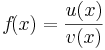
=> 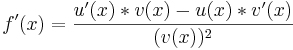
Kettenregel
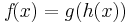
=> 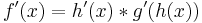
Umkehrregel
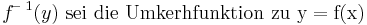
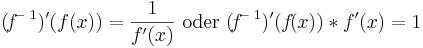
Beispiele
Summenregel
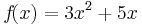
=> 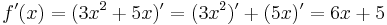
Produktregel
Beispiel 1
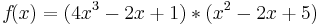
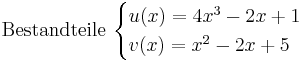
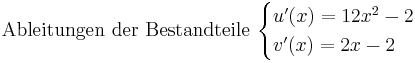
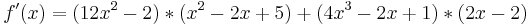
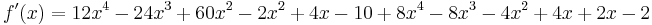
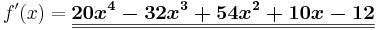
Beispiel 2
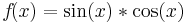
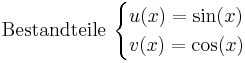
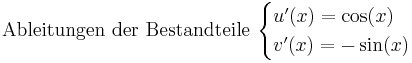
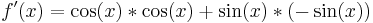
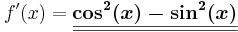
Beispiel 3