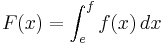Flächenberechnungen: Unterschied zwischen den Versionen
| Zeile 6: | Zeile 6: | ||
-Alle Seiten sind gleichlang.<br /> | -Alle Seiten sind gleichlang.<br /> | ||
-Alle Winkel sind 90°.<br /> | -Alle Winkel sind 90°.<br /> | ||
| − | -Die Diagonalen stehen senkrecht aufeinander, sind gleich lang und halbieren sich. | + | -Die Diagonalen stehen senkrecht aufeinander, sind gleich lang und halbieren sich.<br /> |
| + | |||
| + | Umfang U: <math>U=4*a</math> Flächeninhalt A: <math>A=a^2</math> | ||
| + | |||
| + | |||
'''Rechteck''' | '''Rechteck''' | ||
| Zeile 12: | Zeile 16: | ||
-Gegenüberliegende Seiten sind gleichlang und parallel.<br /> | -Gegenüberliegende Seiten sind gleichlang und parallel.<br /> | ||
-Alle Winkel sind 90°.<br /> | -Alle Winkel sind 90°.<br /> | ||
| − | -Die Diagonalen sind gleich lang und halbieren sich. | + | -Die Diagonalen sind gleich lang und halbieren sich.<br /> |
| + | |||
| + | Umfang U: <math>U=2*(a+b)</math> Flächeninhalt A: <math>A=a*b</math> | ||
'''Dreieck''' | '''Dreieck''' | ||
| − | -Die Summe der Innenwinkel beträgt 180°. | + | -Die Summe der Innenwinkel beträgt 180°.<br /> |
| + | |||
| + | Umfang U: <math>U=a+b+c</math> Flächeninhalt A: <math>A=\frac{a*h_a}{2}</math> <math>A=\frac{b*h_b}{2}</math> <math>A=\frac{c*h_c}{2}</math> | ||
'''Parallelogramm''' | '''Parallelogramm''' | ||
| Zeile 22: | Zeile 30: | ||
-Gegenüberliegende Seiten sind gleichlang und parallel.<br /> | -Gegenüberliegende Seiten sind gleichlang und parallel.<br /> | ||
-Gegenüberliegende Winkel sind gleich groß.<br /> | -Gegenüberliegende Winkel sind gleich groß.<br /> | ||
| − | -Die Diagonalen halbieren sich. | + | -Die Diagonalen halbieren sich.<br /> |
| + | |||
| + | Umfang U: <math>U=2*(a+b)</math> Flächeninhalt A: <math>A=a*h_a</math> <math>A=b*h_b</math> | ||
'''Trapez''' | '''Trapez''' | ||
| − | -Grund- und Decklinien sin parallel. | + | -Grund- und Decklinien sin parallel.<br /> |
| + | |||
| + | Umfang U: <math>U=a+b+c+d</math> Flächeninhalt A: <math>A=\frac{a+c}{2}*h</math> | ||
'''Raute''' | '''Raute''' | ||
| Zeile 32: | Zeile 44: | ||
-Alle Seiten sind gleichlang.<br /> | -Alle Seiten sind gleichlang.<br /> | ||
-Gegenüberliegende Winkel sind gleich groß.<br /> | -Gegenüberliegende Winkel sind gleich groß.<br /> | ||
| − | -Die Diagonalen stehen senkrecht aufeinander. | + | -Die Diagonalen stehen senkrecht aufeinander.<br /> |
| + | |||
| + | Umfang U: <math>U=4*a</math> Flächeninhalt A: <math>A=a*h_a</math> | ||
| + | |||
| + | '''Drachen''' | ||
| + | |||
| + | -Die benachbarten Seiten sind gleichlang.<br /> | ||
| + | -Gegenüberliegende Winkel sind gleich groß.<br /> | ||
| + | -Die Diagonalen stehen senkrecht aufeinander.<br /> | ||
| + | |||
| + | Umfang U: <math>U=2*(a+b)</math> Flächeninhalt A: <math>A=\frac{e*f}{2}</math> | ||
'''Kreis''' | '''Kreis''' | ||
| Zeile 38: | Zeile 60: | ||
-Alle Punkte auf der Kreislinie haben vom Mittelpunkt M den gleichen Abstand.<br /> | -Alle Punkte auf der Kreislinie haben vom Mittelpunkt M den gleichen Abstand.<br /> | ||
-Der Abstand vom Mittelpunkt M zur Kreislinie ist der Radius.<br /> | -Der Abstand vom Mittelpunkt M zur Kreislinie ist der Radius.<br /> | ||
| − | -Der Abstand von einem Punkt der Kreislinie durch den Mittelpunkt M zum gegenüberliegenden Punkt der Kreislinie ist der Durchmesser d. | + | -Der Abstand von einem Punkt der Kreislinie durch den Mittelpunkt M zum gegenüberliegenden Punkt der Kreislinie ist der Durchmesser d.<br /> |
| + | |||
| + | Umfang U: <math>U=2*r*\pi</math> Flächeninhalt A: <math>A=\pi*r^2</math> | ||
Version vom 3. Dezember 2009, 11:31 Uhr
Flächenberechnung:
Quadrat
-Alle Seiten sind gleichlang.
-Alle Winkel sind 90°.
-Die Diagonalen stehen senkrecht aufeinander, sind gleich lang und halbieren sich.
Umfang U: 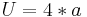 Flächeninhalt A:
Flächeninhalt A: 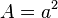
Rechteck
-Gegenüberliegende Seiten sind gleichlang und parallel.
-Alle Winkel sind 90°.
-Die Diagonalen sind gleich lang und halbieren sich.
Umfang U: 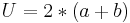 Flächeninhalt A:
Flächeninhalt A: 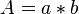
Dreieck
-Die Summe der Innenwinkel beträgt 180°.
Umfang U: 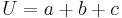 Flächeninhalt A:
Flächeninhalt A: 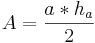
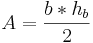
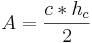
Parallelogramm
-Gegenüberliegende Seiten sind gleichlang und parallel.
-Gegenüberliegende Winkel sind gleich groß.
-Die Diagonalen halbieren sich.
Umfang U: 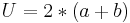 Flächeninhalt A:
Flächeninhalt A: 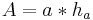
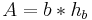
Trapez
-Grund- und Decklinien sin parallel.
Umfang U: 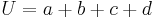 Flächeninhalt A:
Flächeninhalt A: 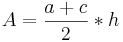
Raute
-Alle Seiten sind gleichlang.
-Gegenüberliegende Winkel sind gleich groß.
-Die Diagonalen stehen senkrecht aufeinander.
Umfang U: 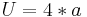 Flächeninhalt A:
Flächeninhalt A: 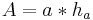
Drachen
-Die benachbarten Seiten sind gleichlang.
-Gegenüberliegende Winkel sind gleich groß.
-Die Diagonalen stehen senkrecht aufeinander.
Umfang U: 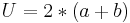 Flächeninhalt A:
Flächeninhalt A: 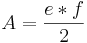
Kreis
-Alle Punkte auf der Kreislinie haben vom Mittelpunkt M den gleichen Abstand.
-Der Abstand vom Mittelpunkt M zur Kreislinie ist der Radius.
-Der Abstand von einem Punkt der Kreislinie durch den Mittelpunkt M zum gegenüberliegenden Punkt der Kreislinie ist der Durchmesser d.
Umfang U: 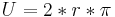 Flächeninhalt A:
Flächeninhalt A: 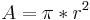
Berechnung von Flächen durch Integrale
Gesucht ist der Flächeninhalt den eine gegebene Funktion mit einer anderen Funktion oder der x-Achse einschließt.
Der erste Schritt besteht darin das Intervall festzulegen in dem die Fläche berechnet wird, dabei gibt es drei Unterscheidungen.
1. Funktion und x-Achse: Berechnen der Nullstellen wobei die erhaltenen Werte das Intervall bilden
2. Funktion und Funktion: Berechnen der Schnittstellen wobei die erhaltenen Werte das Intervall bilden
3.Funktion und lim: Das Intervall geht gegen 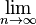
Formeln
Gesucht ist Flächeninhalt zwischen 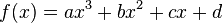 und der x-Achse mit dem Intervall [e;f] wobei e und f die Nullstellen der Funktion sind.
und der x-Achse mit dem Intervall [e;f] wobei e und f die Nullstellen der Funktion sind.