Diskussion zur Struktur der Integralrechnung: Unterschied zwischen den Versionen

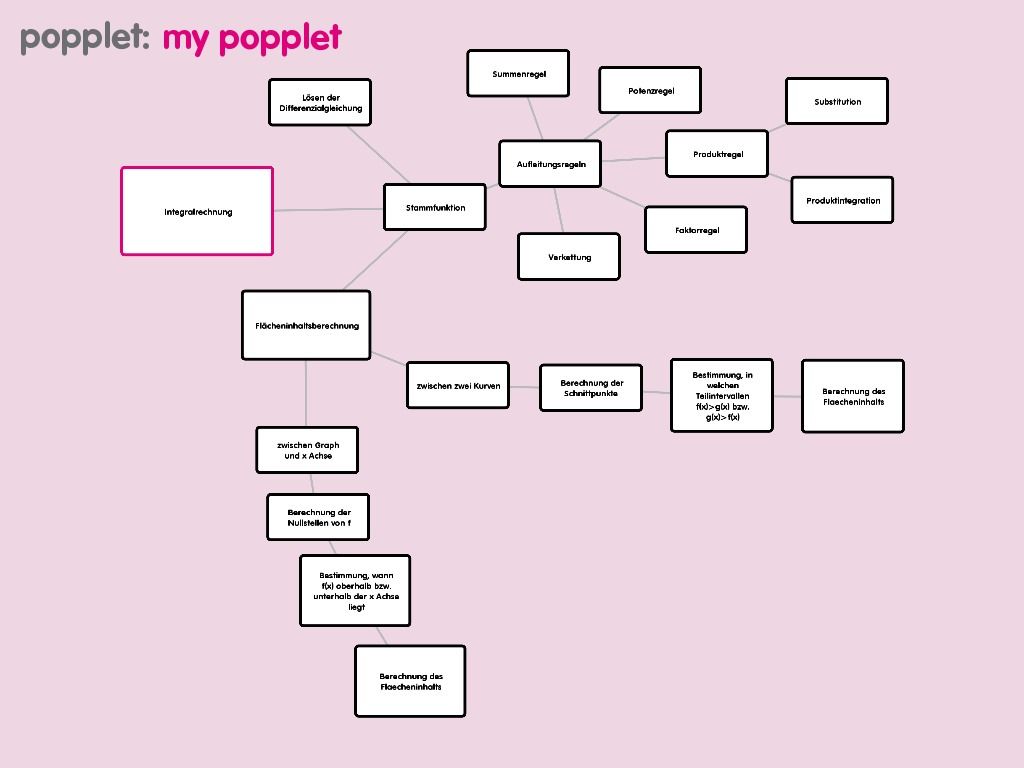
-die 2 Methoden zur Flächeninhaltsberechnung finde ich sehr übersichtlich und hilfreich, da zu den jeweiligen Methoden die einzelnen Schritte der Vorgehensweise beschrieben wird

-Substitution nicht nur als Lösung der Produktregel

-(s.o.)Hää? ist die Substitution nicht eine Integrationsmethode für Produkte mit Kettenregel und somit eine Lösung der Produktregel??

Vorschläge: - Ich persönlich würde in diese Mind Map die Eigenschaften von der unteren Mind Map einbauen

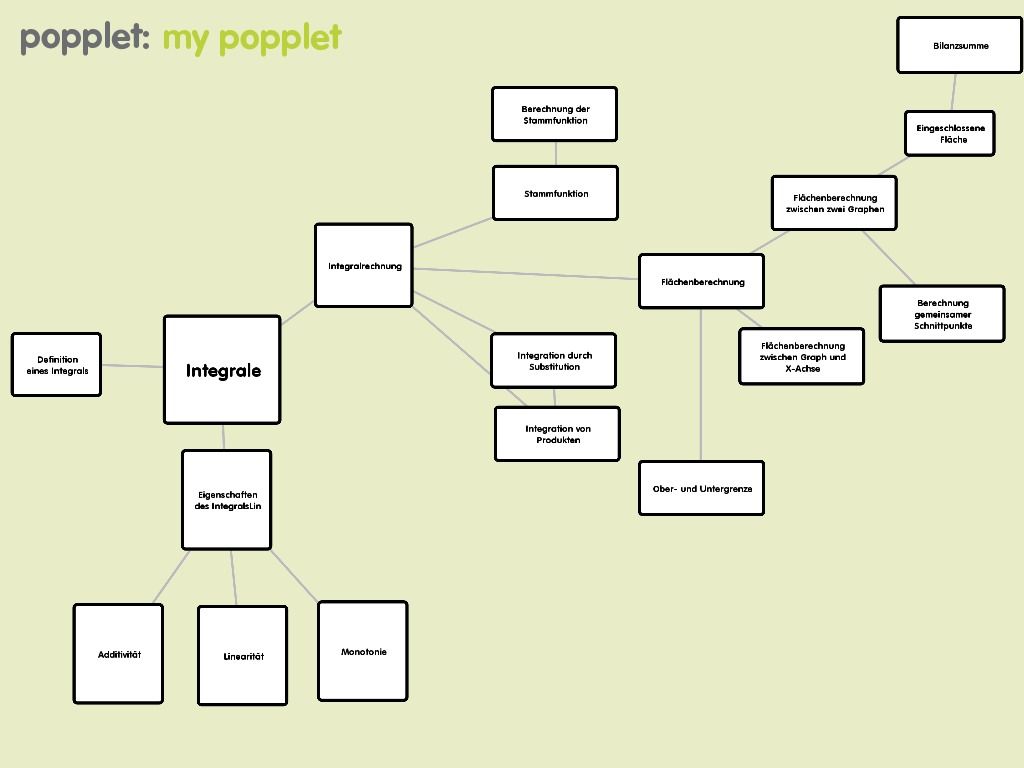
-gut finde ich, dass diese Gruppe auch auf die Eigenschaften und die Bedeutung der Integrale eingeht.Das müsste nämlich eigentlich der erste Schritt sein, dass man klärt was überhaupt ein Integral ist und was uns das sagt und dann nämlich auf die ganzen Regeln und Methoden eingeht...

-Vielleicht kann man Definition und Eigenschaften noch etwas weiter ausführen, damit man in einem Jahr immer noch weiß was damit gemeint ist- -warum sind produktintegration und substitution von berechnung der stammfkt getrennt? -warum steht da nur definition des integrals und nicht DIE definition => es fehlen die zusammenhänge

Vorschläge: Man sollte diese Mindmap als Midmap für unser Wiki nutzen, jedoch mit kleinen Veränderungen und Ergänzungen.

-Ich finde gut, das genauer differenziert wird, wo und wie man Integrale ausrechnen kann, dass zum Beispiel erklärt ist, wie man den Flächeninhalt zwischen zwei verschiedenen Funktionen ausrechnet

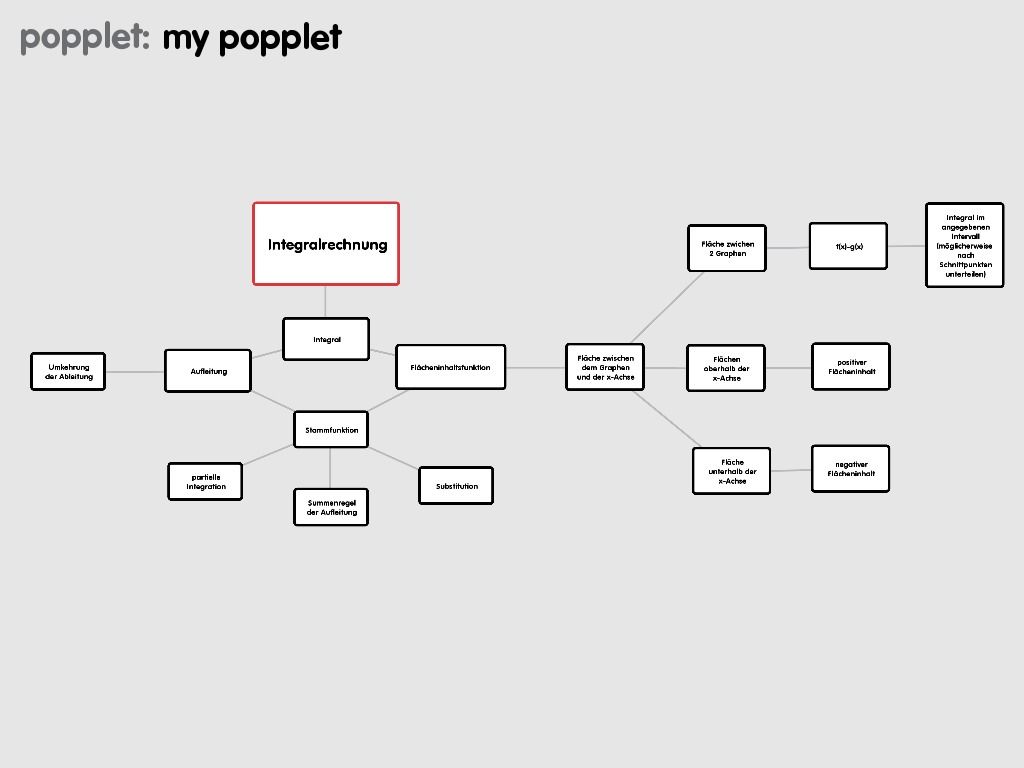
-bei der gesuchten Fläche zwischen 2 Graphen gilt nicht immer f(x)-g(x), dies gilt nämlich nur wenn f(x)>g(x) ist.also muss zunächst bestimmt werden, in welchen Teilintervallen f(x)>g(x) bzw. g(x)>f(x) gilt.-> doch weil man am besten den betrag nutzt

Vorschläge: Die ersten drei MInd -Maps sehen sehr ähnlich aus. Man müsste sie miteinander vergleichen und nur noch ein wenig ergänzen, denn vom Aufbau finde ich sie übersichtlich und gut strukturiert. Die letzte Mind- Map finde ich persönlich zu unübersichtlich.

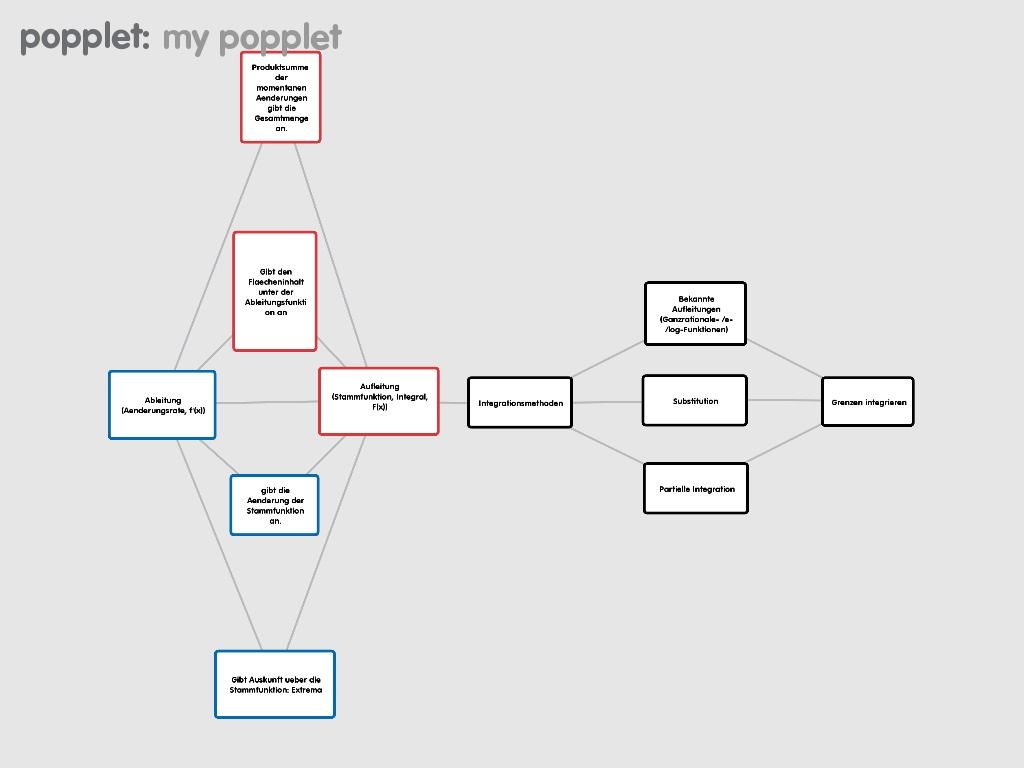
-den schwarz markierten Teil finde ich sehr gelungen, da die verschiedenen Integrationsmethoden genannt werden
-die farbunterteilung ist eine gute idee, aber in einem jahr werden wir das nicht mehr verstehen

-die aufgeführte Integrationsmethode mit den bekannten Aufleitungen würde ich noch näher ausführen, in dem man vielleicht nochmal die wichtigsten Aufleitungsregeln auflistet

-in den blauen und rosafarbenen Kästchen sehe ich keinen Sinn. Die Begriffe der Ableitung und Stammfunktion sind zwar wichtige Begriffe bei der Integralrechnung, aber was hat das mit den Extrema zu tun????????
-Dem stimme ich zu, um diese Struktur zu verstehen, bedarf es folgender Erklärung: Die Blauen Kästen verdeutlichen die Informationen, die man durch die Ableitung über die Stammfunktion erfahren kann. Die Roten dagegen symbolisieren die Informationen, die die Stammfunktion über die Ableitung gibt. Das ganze müsste irgendwie mit Pfeilen deutlicher kenntlich gemacht werden. - Ich finde die Mind Map ein wenig zu kompliziert gestaltet und denke dass man in einem Jahr davon nichts mehr versteht. Man sollte die ersten 3 Mind Maps nehmen und zusammen zu einer gestalten. - Ich finde die Mind Map ein bischen zu unausführlich, die würde ich persönlich nach einem Jahr nicht mehr verstehen

Vorschläge: