Gebrochene rationale Funktionen.: Unterschied zwischen den Versionen
Aus KAS-Wiki
Anabel (Diskussion | Beiträge) (→Defition von gebrochenrationalen Funktionen) |
Anabel (Diskussion | Beiträge) (→Defition von gebrochenrationalen Funktionen) |
||
| Zeile 1: | Zeile 1: | ||
== Defition von gebrochenrationalen Funktionen == | == Defition von gebrochenrationalen Funktionen == | ||
| − | Eine gebrochenrationale Funtion ist ein Bruch zweier ganzrationaler Funtionen g(x) und h(x). | + | Eine gebrochenrationale Funtion ist ein Bruch zweier ganzrationaler Funtionen g(x) und h(x). |
| − | Dabei heißt g(x) '''Zählerfunktion''' mit dem Zählergrad ZG und h(x) heißt '''Nennerfunktion''' mit | + | Dabei heißt g(x) '''Zählerfunktion''' mit dem Zählergrad ZG und h(x) heißt '''Nennerfunktion''' mit |
| − | dem Nennergrad NG. | + | dem Nennergrad NG. |
'''Allgemeine Form der Funktion:''' f(x) = <math>\frac{g(x)}{h(x)}</math> mit dem ganzrationalen Funktionen | '''Allgemeine Form der Funktion:''' f(x) = <math>\frac{g(x)}{h(x)}</math> mit dem ganzrationalen Funktionen | ||
| Zeile 15: | Zeile 15: | ||
Diese Art von Funktionen nennt man gebrochenrationale Funktion. | Diese Art von Funktionen nennt man gebrochenrationale Funktion. | ||
| − | Ist dagegen <math>h_2</math> = <math>2x^2 + 2</math>, ergibt sich i(x)= <math>\frac{x^3 + x}{2x^2 + 2}</math> = <math>\frac{x(x^2 + 1)}{2(x^2 + 1 }</math> =<math> \frac{x}{2}</math> . | + | Ist dagegen <math>h_2</math> = <math>2x^2 + 2</math>, ergibt sich i(x)=<math>\frac{g(x)}{h_2(x)}</math> = <math>\frac{x^3 + x}{2x^2 + 2}</math> = <math>\frac{x(x^2 + 1)}{2(x^2 + 1 }</math> =<math> \frac{x}{2}</math> . |
Version vom 8. Dezember 2009, 13:13 Uhr
Defition von gebrochenrationalen Funktionen
Eine gebrochenrationale Funtion ist ein Bruch zweier ganzrationaler Funtionen g(x) und h(x). Dabei heißt g(x) Zählerfunktion mit dem Zählergrad ZG und h(x) heißt Nennerfunktion mit dem Nennergrad NG.
Allgemeine Form der Funktion: f(x) =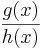 
mit dem ganzrationalen Funktionen
g(x) und h(x) ( Grad h(x) 
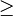1).
Bei einer ganzrationalen ist der Funktionsterm ein Polynom.
Ist z.B. g(x) =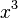 
+ x und 
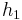(x) =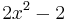 
, ergibt sich f(x) = 
=
= 
.
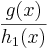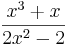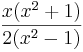Diese Art von Funktionen nennt man gebrochenrationale Funktion.
Ist dagegen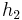 
= 
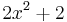, ergibt sich i(x)=
= 
= 
=
.
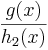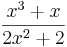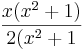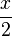