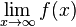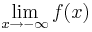Kurvendiskussion.: Unterschied zwischen den Versionen
Aus KAS-Wiki
Radu12 (Diskussion | Beiträge) (→Extrempunkte) |
Radu12 (Diskussion | Beiträge) (→Grenzverhalten) |
||
| Zeile 50: | Zeile 50: | ||
== Grenzverhalten == | == Grenzverhalten == | ||
| − | Der Verlauf des Graphen bei '''<u>unendlich großen bzw. kleinen x-Werten</u>''' wird durch das Grenzverhalten beschrieben. | + | Der Verlauf des Graphen bei '''<u>unendlich großen bzw. unendlich kleinen x-Werten</u>''' wird durch das Grenzverhalten beschrieben. |
Version vom 8. Dezember 2009, 18:08 Uhr
Inhaltsverzeichnis |
Definitionsbereich
Symmetrie
Punktsymmetrie
Alle Exponenten der Funktion sind ungerade.
Achsensymmetrie
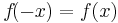
Alle Exponenten der Funktion sind gerade.
Funktionen mit geraden und ungeraden Exponenten weisen keine Symmetrie auf.
Nullstellen
Schnittpunkte der Funktion mit der x-Achse
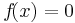
Ableitung
1. Ableitung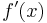 
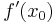gibt die Steigung m im Punkt 
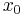an.
2. Ableitung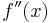 
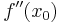gibt die Krümmung vo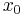n an.
Bei positiven Werten handelt es sich dabei um eine Rechtskrümmung, bei negativen Werten, um eine Linkskrümmung.
3. Ableitung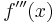 
siehe Ableitungsregeln.
Extrempunkte
In Extrempunkten (Hoch- und Tiefpunkten) ist die Steigung m=0,
deshalb folgt die notwendige Bedingung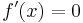 
Wendepunkte
Grenzverhalten
Der Verlauf des Graphen bei unendlich großen bzw. unendlich kleinen x-Werten wird durch das Grenzverhalten beschrieben.
