Ableitungsregeln.: Unterschied zwischen den Versionen

Aus KAS-Wiki
Wechseln zu: Navigation, Suche
(→‎Ableitungen (Ableitungsfunktionen) spezieller Funktionen)
(→‎Ableitungen (Ableitungsfunktionen) spezieller Funktionen)
Zeile 243: Zeile 243:
 
|-
 
|-
 
| <math>\!a^x</math>
 
| <math>\!a^x</math>
−
| <math></math>
+
| <math>\!</math>
−
| <math></math>
+
| <math>\!</math>
 
|-
 
|-
−
| <math></math>
+
| <math>\!/sin x</math>
−
| <math></math>
+
| <math>\!/cos x</math>
−
| <math></math>
+
| <math>\! /-sin x</math>
 
|-
 
|-
−
| <math></math>
+
| <math>\!</math>
−
| <math></math>
+
| <math>\!</math>
−
| <math></math>
+
| <math>\!</math>
 
|-
 
|-
−
| <math></math>
+
| <math>\!</math>
−
| <math></math>
+
| <math>\!</math>
−
| <math></math>
+
| <math>\!</math>
 
|-
 
|-
−
| <math></math>
+
| <math>\!</math>
−
| <math></math>
+
| <math>\!</math>
−
| <math></math>
+
| <math>\!</math>
 
|-
 
|-
−
| <math></math>
+
| <math>\!</math>
−
| <math></math>
+
| <math>\!</math>
−
| <math></math>
+
| <math>\!</math>
 
|-
 
|-
−
| <math></math>
+
| <math>\!</math>
−
| <math></math>
+
| <math>\!</math>
−
| <math></math>
+
| <math>\!</math>
 
|}
 
|}

Version vom 14. Dezember 2009, 10:31 Uhr

Inhaltsverzeichnis

Ableitungsregeln

Potenzregel

f\!(x)=x^n

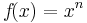
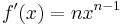
=> f\!\,'(x)=nx^{n-1}


Beispiel

f\!(x)=x^2

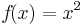
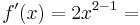
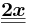
=> f\!\,'(x)=2x^{2-1}=\!\,\boldsymbol{\underline{\underline{2x}}}

Summenregel

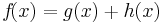
f\!(x)=g(x)+h(x)

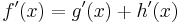
=> f\!\,'(x)=g'(x)+h'(x)


Beispiel

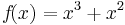
f\!(x)=x^3+x^2

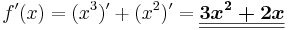
=> f\!\,'(x)= (x^3)' + (x^2)' = \boldsymbol{\underline{\underline{3x^2 + 2x}}}


Faktorregel

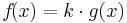
f\!(x)=k \cdot g(x)

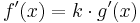
=> f\!\,'(x)=k \cdot g'(x)


Beispiel

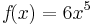
f\!(x)=6x^5

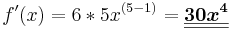
=> f\!\,'(x)=6*5x^{(5-1)} = \boldsymbol{\underline{\underline{30x^4}}}


Differenzregel

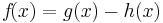
f\!(x)=g(x)-h(x)

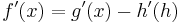
=> f\!\,'(x)=g'(x)-h'(h)


Beispiel

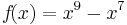
f\!(x)=x^9-x^7

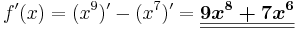
=> f\!\,'(x)= (x^9)' - (x^7)' = \boldsymbol{\underline{\underline{9x^8 + 7x^6}}}


Produktregel

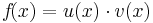
f\!(x)=u(x) \cdot v(x)

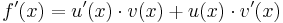
=> f\!\,'(x)=u'(x) \cdot v(x)+u(x) \cdot v'(x)


Beispiel 1

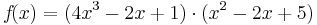
f\!(x)=(4x^3-2x+1) \cdot (x^2-2x+5)


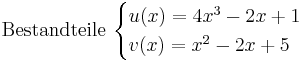
\mathrm{Bestandteile}\ \begin{cases} u(x)=4x^3-2x+1\\ v(x)=x^2-2x+5 \end{cases}


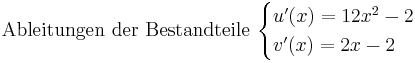
\mathrm{Ableitungen\ der\ Bestandteile}\ \begin{cases} u'(x)=12x^2-2\\ v'(x)=2x-2 \end{cases}


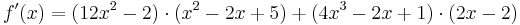
f\!\,'(x)=(12x^2-2) \cdot (x^2-2x+5)+(4x^3-2x+1) \cdot (2x-2)

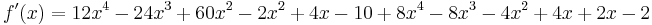
f\!\,'(x)=12x^4-24x^3+60x^2-2x^2+4x-10+8x^4-8x^3-4x^2+4x+2x-2

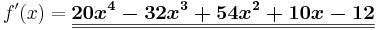
f\!\,'(x)=\boldsymbol{\underline{\underline{20x^4-32x^3+54x^2+10x-12}}}


Beispiel 2

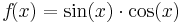
f\!(x)=\sin(x) \cdot \cos(x)

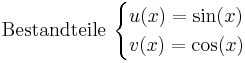
\mathrm{Bestandteile}\ \begin{cases} u(x)=\sin(x)\\ v(x)=\cos(x) \end{cases}


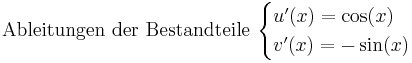
\mathrm{Ableitungen\ der\ Bestandteile}\ \begin{cases} u'(x)=\cos(x)\\ v'(x)=-\sin(x) \end{cases}


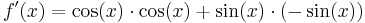
f\!\,'(x)=\cos(x) \cdot \cos(x)+\sin(x) \cdot (-\sin(x))

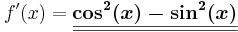
f\!\,'(x)=\boldsymbol{\underline{\underline{\cos^2(x)-\sin^2(x)}}}


Beispiel 3

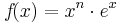
f\!(x)=x^n \cdot e^{x}

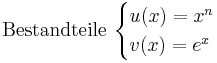
\mathrm{Bestandteile}\ \begin{cases} u(x)=x^n\\ v(x)=e^{x} \end{cases}


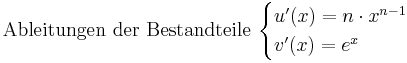
\mathrm{Ableitungen\ der\ Bestandteile}\ \begin{cases} u'(x)=n \cdot x^{n-1}\\ v'(x)=e^{x} \end{cases}


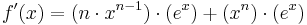
f\!\,'(x)=(n \cdot x^{n-1}) \cdot (e^{x})+(x^n) \cdot (e^{x})

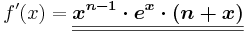
f\!\,'(x)=\boldsymbol{\underline{\underline{x^{n-1} \cdot e^{x} \cdot (n+x)}}}


Quotientenregel

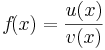
f\!(x)=\frac{u(x)}{v(x)}

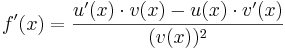
=> f\!\,'(x)=\frac{u'(x) \cdot v(x)-u(x) \cdot v'(x)}{(v(x))^2}


Beispiel

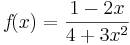
f\!(x)=\frac{1-2x}{4+3x^2}

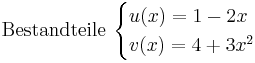
\mathrm{Bestandteile}\ \begin{cases} u(x)=1-2x\\ v(x)=4+3x^2 \end{cases}


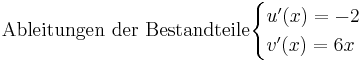
\mathrm{Ableitungen\ der\ Bestandteile} \begin{cases} u'(x)=-2\\ v'(x)=6x \end{cases}


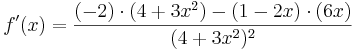
f\!\,'(x)=\frac{(-2) \cdot (4+3x^2)-(1-2x) \cdot (6x)}{(4+3x^2)^2}

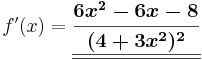
f\!\,'(x)=\boldsymbol{\underline{\underline{\frac{6x^2-6x-8}{(4+3x^2)^2}}}}


Kettenregel

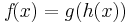f\!(x)=g(h(x)) bzw. f\!(x)=g(u) mit u=h\!(x)

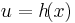
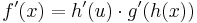
=> f\!\,'(x)=h'(u) \cdot g'(h(x))

Die Ableitung von einer verketteten Funktion wird grob gesagt gebildet, indem man erst die äußere Ableitung und dann die innere bildet.

Beispiel 1

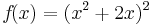
f\!(x) = (x^2 + 2x)^2
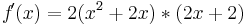
f\! '(x) = 2(x^2 + 2x)*(2x + 2)

Beispiel 2

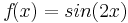
f\!(x)= sin (2x)

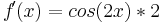
f\! '(x) = cos (2x) * 2

Hilfestellung

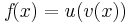
f\!(x) = u(v(x))
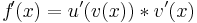
f\! '(x) = u'(v(x)) * v'(x)

Beispiel von oben (2):

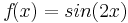
f\! (x) = sin (2x)

u\! = sin u\! ' = cos
v\! = 2x v\! ' = 2


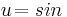
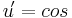
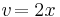
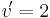
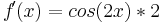
f\! '(x) = cos (2x) * 2
Also: 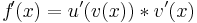f\! '(x) = u' (v(x)) * v'(x)

Umkehrregel

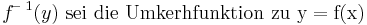
f\!^-\,^1(y)\ \mathrm{sei\ die\ Umkerhfunktion\ zu\ y=f(x)}

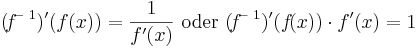
(\!f\!^-\,^1)'(f(x))=\frac{1}{f'(x)}\ \mathrm{oder}\ (\!f\!^-\,^1)'(f\!(x)) \cdot f\!\,'(x)=1


Beispiel

Ableitungen (Ableitungsfunktionen) spezieller Funktionen

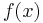
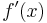
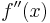
\!f(x) \!f'(x) \!f''(x)
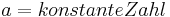
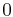
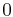
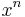
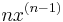
\!a= konstante Zahl \!0 \!0
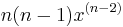
\!x^n \!nx^{(n-1)} \!n(n-1)x^{(n-2)}
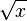
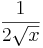
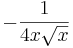
\sqrt{x} \frac{1}{2\sqrt{x}} -\frac{1}{4x\sqrt{x}}
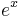
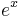
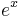
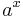
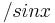
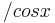
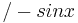
\!e^x \!e^x \!e^x
\!a^x \! \!
\!/sin x \!/cos x \! /-sin x
\! \! \!
\! \! \!
\! \! \!
\! \! \!
\! \! \!
Von „http://kas.zum.de/index.php?title=Ableitungsregeln.&oldid=873“