Ganzrationale Funktionen.: Unterschied zwischen den Versionen
Aus KAS-Wiki
Franca (Diskussion | Beiträge) (→Funktionen 2. Grades:) |
Franca (Diskussion | Beiträge) (→Funktionen 2. Grades:) |
||
| Zeile 39: | Zeile 39: | ||
<math>x_{1,2}</math> = <math>\frac{-p}{2}</math> <math> \pm \sqrt{ (\frac{-p}{2})^2-q }</math> | <math>x_{1,2}</math> = <math>\frac{-p}{2}</math> <math> \pm \sqrt{ (\frac{-p}{2})^2-q }</math> | ||
| − | oder c ist gleich 0: | + | oder c ist gleich 0:<br /> |
| − | ax<sup>2</sup>+bx= 0 | x ausklammern | + | ax<sup>2</sup>+bx= 0 | x ausklammern<br /> |
| − | x(ax+b) = 0 | + | x(ax+b) = 0<br /> |
| − | dann: | + | dann:<br /> |
| − | ax+b = 0 | + | ax+b = 0<br /> |
== Funktionen 3. Grades: == | == Funktionen 3. Grades: == | ||
Version vom 14. Dezember 2009, 11:31 Uhr
Inhaltsverzeichnis |
Ganzrationale Funktionen
f(x) = anxn + an-1xn-1 + ... + a1x + a0
n = Grad des Polynoms
Definitionsbereich:
-
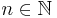
- an
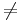0
Bestimmung einer ganzrationalen Funktion in Sachzusammenhängen:
- lineares Gleichungssystem aufstellen und lösen
- Koordinatensystem auswählen
- Bedingung: n + 1 Bedingungen sind nötig
Nullstellen der Funktion:
f(x)=0
Funktionen 2. Grades:
Gleichung f(x)=0 in die Normalform umwandeln:
f(x)= ax2 + bx + c | :a
= x2 +x +
- Lösen der Gleichung mithilfe der p/q-Formel:
f(x) =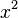 
+ px + q = 0
= 
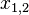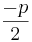
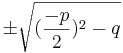
oder c ist gleich 0:
ax2+bx= 0 | x ausklammern
x(ax+b) = 0
dann:
ax+b = 0
Funktionen 3. Grades:
f(x)= a3x + b2x + cx+d
- Lösen der Gleichung mithilfe der Polynomdivision:
