G6: Verschobene Normalparabeln der Form f(x)=(x-d)²: Unterschied zwischen den Versionen
Aus KAS-Wiki
(→Verschobene Normalparabeln der Form f(x)=(x-d)²) |
(→Verschobene Normalparabeln der Form f(x)=(x-d)²) |
||
| Zeile 8: | Zeile 8: | ||
Die Normalparabel ist nach oben geöffnet. | Die Normalparabel ist nach oben geöffnet. | ||
| − | '''Hinweis:''' | + | '''Hinweis:''' eine nach unten geöffnete Parabel wäre -X². |
| − | + | Bei einem Beispiel wie: 1/2 vor dem X² sorgt für eine Verbreiterung der Parabel ebenso wie ein Faktor >1 vor dem X² eine Verschmälerung der Normalparabel verursacht. | |
Version vom 16. Dezember 2009, 09:41 Uhr
Verschobene Normalparabeln der Form f(x)=(x-d)²
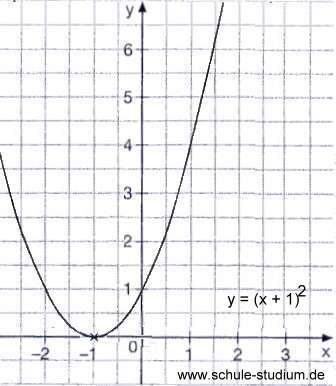
Der Graph von der quadratischen Funktion f mit der Funktionsgleichung y = (x+1)² ist eine nach links verschobene Normalparabel. Im Scheitelpunkt S(-1/0) der Normalparabel nimmt die Funktion f den kleinsten Funktionswert an.
Die Normalparabel ist nach oben geöffnet. Hinweis: eine nach unten geöffnete Parabel wäre -X². Bei einem Beispiel wie: 1/2 vor dem X² sorgt für eine Verbreiterung der Parabel ebenso wie ein Faktor >1 vor dem X² eine Verschmälerung der Normalparabel verursacht.