Flächenberechnungen.: Unterschied zwischen den Versionen
Mehmet (Diskussion | Beiträge) (→Kreis) |
Mehmet (Diskussion | Beiträge) |
||
| Zeile 59: | Zeile 59: | ||
;Formel: d= 2r | ;Formel: d= 2r | ||
: u= 2<math>\pi</math>r=<math> \pi</math>d | : u= 2<math>\pi</math>r=<math> \pi</math>d | ||
| − | : A=<math> \pi</math>r²= <math>\frac{\pi}{4} </math>d²[[Kategorie:Geometrie]] | + | : A=<math> \pi</math>r²= <math>\frac{\pi}{4} </math>d²[[Kategorie:Geometrie]]<br /> |
| + | <br /> | ||
| + | == Berechnung von Flächen durch Integrale == | ||
| + | Um die Größe eines Flächeninhalts auszurechen, müssen zunächst einmal die Intervalle bestimmt werden. Wird beispielsweise die Fläche von der Funktion f(x) und der X- Achse eingeschlossen, so müssen erst die Nullstellen berechnet werden, wobei die Nullstellen gleichzeitig die Intervalle sind. <br /> | ||
| + | Bei der Integralrechnung können drei verschiedene Fälle eintreten:<br /> | ||
| + | <br /> | ||
| + | 1. Flächeninhalt zwischen der Funktion f(x) und der x-Achse<br /> | ||
| + | 2. Flächeninhalt zwischen zwei Graphen<br /> | ||
| + | 3. Flächeninhalt | ||
Version vom 18. Dezember 2009, 10:50 Uhr
Inhaltsverzeichnis |
Rechteck
Die Diagonale sind gleich lang und halbieren einander.
Alle Innenwinkel sind gleich groß (90°).
Gegenüberliegende Seiten sind zueinander parallel und gleich lang.
- Formel
- u= 2(a+b)
- A= ab
Quadrat
Die Diagonalen sind zueinander senkrecht, gleich lang und halbierende einander.
Alle Innenwinkel sind gleich groß (90°).
Alles Seiten sind gleich lang.
- Formel
- u= 4a
- A= a²=
 c²
c²
Trapez
Mindestens zwei Seiten sind zueinander parallel.
- Formel
- u= a+b+c+d
- A= mh=
 (a+c)h
(a+c)h
Parallellogramm
Die Diagonale halbieren einander.
Gegenüberliegende Winkel sind gleich groß.
Gegenüberliegende Seiten sind zueinander parallel und gleich lang.
- Formel
- u= 2(a+b)
- A= aha= ab sin
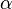
Drache
Die Diagonalen sind zueinander senkrecht.
Mindestens zwei gegenüberliegende Winkel sind gleich groß.
- Formel
- u= 2(a+c)
- A=
 ef
ef
Kreis
Der Mittelpunkt M hat zu allen Punkten auf der Kreislinie den gleichen Abstand.
Der Abstand vom Mittelpunkt M bis zur Kreislinie nennt man Radius r.
Der doppelte Radius ist gleichzeitig der Durchmesser.
- Formel
- d= 2r
- u= 2
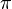 r=
r=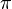 d
d
- A=
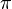 r²=
r²= 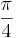 d²
d²
Berechnung von Flächen durch Integrale
Um die Größe eines Flächeninhalts auszurechen, müssen zunächst einmal die Intervalle bestimmt werden. Wird beispielsweise die Fläche von der Funktion f(x) und der X- Achse eingeschlossen, so müssen erst die Nullstellen berechnet werden, wobei die Nullstellen gleichzeitig die Intervalle sind.
Bei der Integralrechnung können drei verschiedene Fälle eintreten:
1. Flächeninhalt zwischen der Funktion f(x) und der x-Achse
2. Flächeninhalt zwischen zwei Graphen
3. Flächeninhalt

