Lösung linearer Gleichungssysteme.: Unterschied zwischen den Versionen
Chris1 (Diskussion | Beiträge) (→Gaußches Eliminierungsverfahren) |
Chris1 (Diskussion | Beiträge) (→Bedingung) |
||
| Zeile 6: | Zeile 6: | ||
* Addition/Subtraktion des Vielfachen einer Gleichung mit einer anderen Gleichung | * Addition/Subtraktion des Vielfachen einer Gleichung mit einer anderen Gleichung | ||
| − | === Bedingung === | + | === Bedingung ===<br /> |
Man braucht mindestens genauso viele Gleichungen, wie unbekannte Variablen. | Man braucht mindestens genauso viele Gleichungen, wie unbekannte Variablen. | ||
| − | Wenn es mehr Gleichungen sind, muss man mit der/den "überflüssigen" Gleichung(en) die Variablen einsetzen und das Ergebniss überprüfen. Wenn die Zahlen nicht übereinsstimmen, gibt es kein Ergebniss. | + | Wenn es mehr Gleichungen sind, muss man mit der/den "überflüssigen" Gleichung(en) die Variablen einsetzen und das Ergebniss überprüfen. Wenn die Zahlen nicht übereinsstimmen, gibt es kein Ergebniss.<br /> |
| + | |||
| + | Wenn man mehr unbekannte Variablen hat als Gleichunge ist das Verfahren '''unterbestimmt''' und deshalb '''unlösbar'''. | ||
=== Beispiel === | === Beispiel === | ||
Version vom 18. Dezember 2009, 11:05 Uhr
Inhaltsverzeichnis |
Gaußches Eliminierungsverfahren
Die Operationen
- Multiplikation einer Gleichung mit einem Faktor
- Addition/Subtraktion des Vielfachen einer Gleichung mit einer anderen Gleichung
=== Bedingung ===
Man braucht mindestens genauso viele Gleichungen, wie unbekannte Variablen.
Wenn es mehr Gleichungen sind, muss man mit der/den "überflüssigen" Gleichung(en) die Variablen einsetzen und das Ergebniss überprüfen. Wenn die Zahlen nicht übereinsstimmen, gibt es kein Ergebniss.
Wenn man mehr unbekannte Variablen hat als Gleichunge ist das Verfahren unterbestimmt und deshalb unlösbar.
Beispiel
Aufstellen des linearen Gleichungssystems.
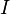
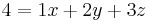
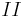
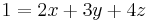
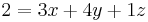
Durch das Subtraktionsverfahren eliminiert man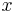 
aus 2 Gleichungen
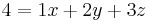
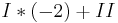
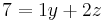
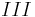
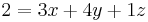
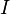
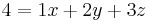
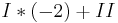
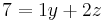
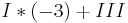
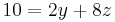
Durch erneute Subtraktion wird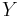 
eliminiert.
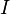
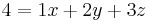
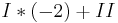
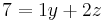
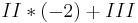
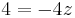
Durch Einsetzten und Lösen erhält man:
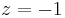
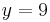
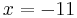
Besonderes
1.Beispiel
Hätte man als Gleichungen:
1. Gleichung: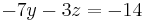 
2. Gleichung: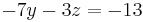 
hätte man nach dem Gleichsetzen das Ergebniss: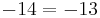 
In solchen Fällen gibt es keine Lösung.
2.Beispiel
Hätte man jedoch die GLeichungen:
1. Gleichung: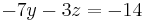
2. Gleichung: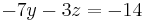
hätte man das Ergebniss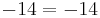 
In solchen Fällen gibt es unendlich viele Lösungen.
